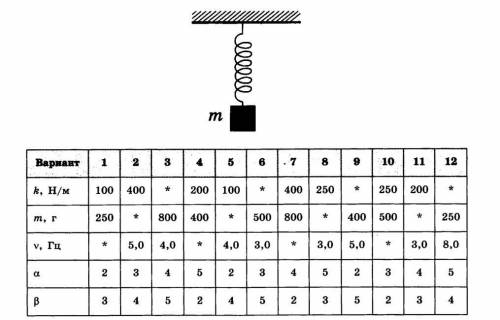
К пружине жесткостью k прикрепили груз массой m (рисунок). Если, слегка растянув пружину, вывести груз из положения равновесия, то он будет совершать колебания с частотой ν. Определите значение величины,обозначенной *. Как изменится частота колебаний, если увеличить массу груза в α раз, а жесткость в β раз? Считать, что колебания груза остану
5 вариант
Другие вопросы по теме Физика
Популярные вопросы
- 1- с раствором соляной кислоты не реагирует: 1. оксид калия 2....
2 - Периметр квадрата равен 16 см. найдите его площадь...
2 - Впараллелограмме abcd сторона ab равна 3 сантиметра,а сторона...
3 - Напишите уравнение реакции дихлоралкана с водным раствором едкого...
2 - Завтра контрольная: в равнобедренном треугольнике авс, ав=вс,проведена...
1 - 1. укажите словосочетание со страдательным причастием: 1)берущиеся...
3 - Circle the correct word. then write short answers....
1 - Треугольники abc и adc лежат в разных плоскостях и имеют общую...
3 - Пліз, іть. що таке: індульгенція, ії, ....
2 - Написать программу которая по трём сторонам треугольника определяло...
2
T = 2π √(m/k)
Где T - период колебаний, m - масса груза, k - жесткость пружины.
Из условия задачи известно, что груз будет совершать колебания с частотой ν. Частота колебаний (f) и период (T) связаны следующей формулой:
f = 1/T
Период колебаний пружины при массе m и жесткости k будет:
T1 = 2π √(m/k)
Если увеличить массу груза в α раз, то новая масса груза будет αm. Если жесткость пружины увеличивается в β раз, то новая жесткость будет βk. Тогда новый период колебаний будет:
T2 = 2π √((αm)/(βk))
Сравнивая формулы для T1 и T2, мы видим, что новый период колебаний T2 различается от первоначального периода T1 только коэффициентом α/β под корнем.
Тогда новая частота колебаний будет:
f2 = 1/T2
f2 = 1/(2π √((αm)/(βk)))
f2 = √((βk)/(αm))/(2π)
Таким образом, частота колебаний изменится по формуле √((βk)/(αm))/(2π).
Чтобы определить значение величины, обозначенной * предлагается проанализировать варианты ответов и выбрать наиболее подходящий.
Итак, для данной задачи:
Значение величины, обозначенной * определяется с помощью формулы √((βk)/(αm))/(2π).
Изменение частоты колебаний при изменении массы груза в α раз и жесткости пружины в β раз определяется формулой √((βk)/(αm))/(2π).