Из пунктов а и в, расстояние между которыми 500 м, навстречу друг другу по прямой дороге идут два брата с одинаковой скоростью 5 км/ч. от одного брата к другому бежит их собака, которая, добежав, немедленно поворачивает и мчится к первому брату. это повторяется, пока братья не встретятся. определите перемещение собаки и пройденный ею путь, если скорость движения собаки 20 км/ч.

Дано:

м = км

км/ч

км/ч

Найти: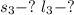

Решение. 1) Выберем систему отсчета "Брат 1". Согласно закону сложения скоростей для Брата 2 скорость составляет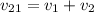 . А выглядит это так: пока Брат 1 находится на месте, Брат 2 самостоятельно преодолевает дистанцию со скоростью 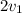, значит, время к моменту встречи равен

Вернемся в систему отсчета "пункт А". Брат 1 за время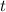 до места встречи пройдет расстояние, которое будет равняться перемещению собаки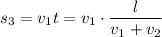

Бегая без остановок на протяжении времени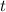 , собака преодолевает путь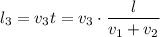

Определим значения искомых величин:

м

м

ответ: 250 м; 1 км