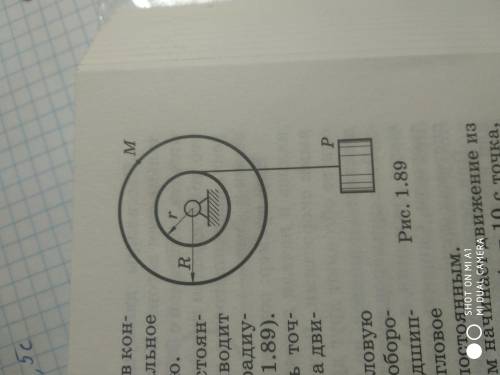
Груз P начинает опускаться с постоянным ускорением а=2м/с² и приводит в движение ступенчатый шкиф радиуосм r=0.25 м И R=0.5 м . Какое ускорение (а1) будет иметь точка М через t=0.5 с после начала движения ? ответ 8.9

Мякишев упр 5 задача 9

Для решения данной задачи, мы можем использовать законы динамики и закон сохранения энергии.

Из условия задачи, у нас есть начальное ускорение а = 2 м/с², радиусы шкифов r1 = 0.25 м и r2 = 0.5 м, и время t = 0.5 с.

1. Посмотрим на систему шкифов и груза. Обозначим силу трения, действующую между грузом и шкифом равной Fт. Также обозначим массу груза P как m, массу шкифов как M и массу груза P + шкифов как М.

2. Найдем силу трения Fт между грузом и шкифом. Для этого воспользуемся первым законом Ньютона: Fт = m * а. Подставим известные значения: Fт = m * 2 м/с².

3. Найдем силу F1, с которой действует груз на шкиф меньшего радиуса (r1). Воспользуемся формулой для центростремительной силы: F1 = m * a1, где a1 - искомое ускорение точки М через t = 0.5 с.

4. Найдем силу F2, с которой груз действует на шкиф большего радиуса (r2). Воспользуемся формулой для центростремительной силы: F2 = M * a2, где a2 - искомое ускорение точки М через t = 0.5 с.

5. Поскольку шкифы имеют одну общую систему и не покидают ее, сила F1 должна равняться силе F2: F1 = F2.

6. Поскольку система шкифов и груза является потенциальной системой, можно использовать закон сохранения энергии: механическая энергия системы в начальный момент должна быть равна механической энергии в момент t = 0.5 с.

7. Механическая энергия системы в начальный момент можно выразить как сумму силы тяжести и потенциальной энергии на высоте h: мgh, где m - масса груза, g - ускорение свободного падения и h - начальная высота груза.

8. Механическая энергия системы через t = 0.5 с состоит из кинетической энергии и потенциальной энергии на высоте h - r1, где h - начальная высота груза и r1 - радиус шкифа меньшего радиуса.

9. Записываем уравнение сохранения энергии: мgh = (1/2) * m * (v1)² + (1/2) * M * (v2)² + mg * (h - r1), где v1 - скорость точки М на шкифе меньшего радиуса и v2 - скорость точки М на шкифе большего радиуса.

10. Выразим скорости v1 и v2 через ускорения a1 и a2: v1 = a1 * t и v2 = a2 * t, где t - время.

11. Подставим найденные значения в уравнение сохранения энергии и решим его относительно a1.

12. Решим полученное уравнение и найдем значение a1.

Данный алгоритм решения задачи дает возможность школьнику понять и постепенно решить задачу, применяя физические законы и концепции. Важно пояснить каждый шаг и обосновать использование того или иного закона или формулы.