11. К тонкому стержню в точках 1 и 3 приложены силы F =10н и F2 =30Н. Если расстояния между точками равны, то, чтобы стержень находился в
равновесии, ось вращения должна находиться в точке
1F2
F₁
A)2
B)5
C)4
D)6
20
3
5

C) точка 4

Объяснение:

Чтобы стержень не вращался вокруг некоторой точки, полный момент всех внешних сил относительно этой точки должен быть равен нулю. Из этого условия и определим, через какую точку необходимо провести ось вращения. Поскольку у нас всего две силы, можно сразу заключить, что искомая точка находится справа от точки 3. Иначе обе силы вращали бы рычаг против часовой стрелки, и не уравновешивали бы друг друга.

Обозначим расстояние между любыми двумя соседними точками через ''L'', а расстояние от точки 3 до искомой точки через ''x''. Тогда сила  F2 вращает стержень по часовой стрелке и и ее момент равен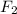 *x. Сила F1 вращает стержень против часовой стрелки, и ее момент равен 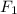*(x + 2L).

Приравняем эти два момента и решим линейное уравнение найдя ''x'':

, т.е. вправо на одно деление, а это точка 4.

Следовательно, ось вращения нужно расположить в точке 4