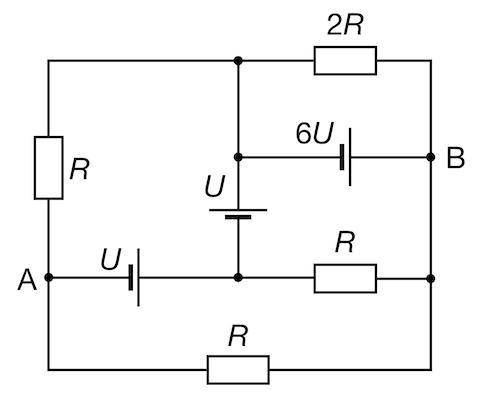
1)Собрана электрическая цепь, схема которой показана на рисунке. Батарейки идеальные, напряжение U=9 В. Чему равно напряжение на резисторе 2R? ответ выразите в вольтах, округлите до целого числа. 2)В условиях предыдущей задачи найдите разность потенциалов φA−φB между точками A и B. ответ выразите в вольтах, округлите до целого числа.
Другие вопросы по теме Физика
Популярные вопросы
- Найдите НОК чисел 25;50;75...
2 - 1. а) Задана пропорция х : 9 = 40 : у. Найдите значение х∙у...
3 - Арап Петра Великого 4 глава 1)Какие новые обычаи вызвали в доме Ржевских...
1 - На прозрачную пленку с показателем преломления 1,5 попадают красные лучи...
3 - Mark the proper form of the verb: İ hope he all the quarrels we have had...
2 - Он сел на лошадьи и поехал в поле,где был клевер Оно простое или сложное?...
2 - Найдите 50 cos2a, если cos a = 0.1...
3 - Могут углы трапеции, взятые последовательно относиться как 5: 4: 6: 3...
3 - Как назывались небольшие египетские государства, состоявшие из объединившихся...
2 - Zoard drink lot of water true false...
1
U = I * R
В данном случае, равенство U = 9 В, а сопротивление резистора 2R.
Мы не знаем силу тока, поэтому воспользуемся законом Кирхгофа. По закону Кирхгофа для узла A справедливо:
U = I1 * R1 + I2 * R2
где I1 и I2 - силы токов в ветвях сопротивлений R1 и R2 соответственно.
Но, поскольку в данной схеме электрической цепи идеальные батарейки, сила тока I будет одинакова во всей цепи. То есть I1 = I2.
Таким образом, уравнение можно переписать в виде:
U = I * (R1 + R2)
I * (R1 + R2) = 9 В
I = 9 В / (R1 + R2)
Используем эту формулу для определения силы тока I.
Теперь, чтобы найти напряжение на резисторе 2R, мы можем использовать силу тока I и сопротивление 2R:
U(2R) = I * 2R
Т.е. U(2R) = (9 В / (R1 + R2)) * 2R
Приведем уравнение к более простому виду:
U(2R) = 18R / (R1 + R2)
Ответ: напряжение на резисторе 2R равно 18R / (R1 + R2) вольт.
2) Для определения разности потенциалов φA−φB между точками A и B воспользуемся тем, что сумма всех напряжений в закольцованной цепи должна быть равна нулю, согласно законам Кирхгофа.
U(battery) - U(2R) - U(R1) = 0
U(battery) = U(2R) + U(R1)
Из предыдущего задания мы уже знаем значение U(2R). Также, согласно формуле для напряжения на резисторе, мы можем определить U(R1) следующим образом:
U(R1) = I * R1
Т.е. U(R1) = (9 В / (R1 + R2)) * R1
Подставим полученные значения в уравнение:
U(battery) = (18R / (R1 + R2)) + ((9 В / (R1 + R2)) * R1)
Теперь остается только привести это уравнение к более простому виду:
U(battery) = 18R / (R1 + R2) + 9R1 / (R1 + R2)
U(battery) = (18R + 9R1) / (R1 + R2)
Ответ: разность потенциалов φA−φB между точками A и B равна (18R + 9R1) / (R1 + R2) вольт.
Округлим ответы до целого числа и подставим значения R1=6 Ом, R2=2 Ом, R=4 Ом:
1) Напряжение на резисторе 2R = 18R / (R1 + R2) = 18 * 4 / (6 + 2) = 9 В.
2) Разность потенциалов φA−φB между точками A и B = (18R + 9R1) / (R1 + R2) = (18 * 4 + 9 * 6) / (6 + 2) = 45/4 В. Округляем до целого числа - ответ: 11 В.