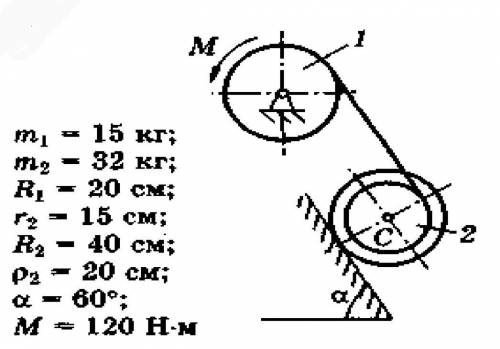
Техмех Определить угловое ускорение тела. Используя теорему об изменении кинетической энергии в дифференциальной форме.
2)Определить угловую скорость тела 1 после его заданного перемещения угол1=2п рад или S1= 2м. Движение начинается из состояния покоя. Использую теорему об изменении кинетической энергии в интегральной форма.

Добрый день! Сегодня в нашем уроке мы рассмотрим определение углового ускорения тела и угловой скорости тела. Для этого мы будем использовать теорему об изменении кинетической энергии в дифференциальной и интегральной форме.

1) Определение углового ускорения тела:

Угловое ускорение тела – это величина, определяющая изменение скорости вращения тела относительно времени. Угловое ускорение обозначается символом α (английская буква "alpha").

Формула для определения углового ускорения тела с использованием теоремы об изменении кинетической энергии в дифференциальной форме имеет вид:

α = dω/dt,

где α - угловое ускорение, dω - изменение угловой скорости тела, dt - изменение времени.

2) Определение угловой скорости тела после заданного перемещения:

Угловая скорость тела – это величина, определяющая скорость вращения тела относительно времени. Угловая скорость обозначается символом ω (английская буква "omega").

Формула для определения угловой скорости тела после заданного перемещения с использованием теоремы об изменении кинетической энергии в интегральной форме выглядит следующим образом:

∫ω1*ω2 dω = ∫0*θ1 α dθ + ∫0*v1 α dt,

где ω1 - начальная угловая скорость, ω2 - конечная угловая скорость, θ1 - заданное перемещение в радианах, α - угловое ускорение тела, v1 - начальная линейная скорость, t - время.

Теперь рассмотрим решение поставленной задачи.

1) Определение углового ускорения тела:

Для определения углового ускорения тела воспользуемся формулой α = dω/dt. Нам необходимо знать изменение угловой скорости и изменение времени. Давайте посмотрим на представленный график скорости (ω) от времени (t), который изображен на рисунке. Мы можем рассчитать угловое ускорение, найдя производную от графика угловой скорости в зависимости от времени.

2) Определение угловой скорости тела после заданного перемещения:

Для определения угловой скорости тела после заданного перемещения воспользуемся формулой ∫ω1*ω2 dω = ∫0*θ1 α dθ + ∫0*v1 α dt. В данной формуле нам необходимо знать начальную и конечную угловую скорость, заданное перемещение в радианах и угловое ускорение. Подставив известные значения, мы сможем рассчитать угловую скорость тела после заданного перемещения.

Вот таким образом, мы определим угловое ускорение тела и угловую скорость тела после заданного перемещения, используя теорему об изменении кинетической энергии в дифференциальной форме и интегральной форме.