Знайдіть найбільше та найменше значення функції y = (x ^ 2 + 4)/(2x - 3) на проміжку [0;5]
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать сочинение Петр 1 карл 12 в поэме Пушкину Полтава...
3 - *прочитайте предложения. перепишите, расставляя знаки препинания. В конце предложения...
3 - 1. Назвіть по три приклади сучасних міст, у назвах яких відображено б їх утворення:...
1 - Сделайте эти 5 задач. Обязательно с решением! От Спаммеров и ботов буду банить....
1 - Ν (C5H12) = моль ν (H2O) = моль m (H2O) = г...
2 - Поетапно еволюцію вогнепальної зброї...
2 - Определи координаты точек А, В, Си D. Используя координаты, найди значение выражения....
3 - мне осталась жить один день я хочу этот 1 день закончить на пять...
3 - Сравните изображение земли на карте полушарий и глобусе. в графах глобус и карта...
2 - четыре силы направлены по одной прямой верх 20 и 30 Н вниз 40 и 30 Н Определите...
2
наибольшее значение функции равно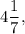 а наименьшее значение функции равно
а наименьшее значение функции равно 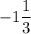
Объяснение:
Найти наибольшее и наименьшее значение функции
Так как делить на нуль нельзя, то 2х -3 ≠0, то есть х ≠ 1,5.
Тогда область определение функции: D(y) = ( -∞ ; 1,5 ) ∪(1,5; + ∞)
Найдем производную функции
Найдем критические точки, решив уравнение: y' = 0.
Дробь равна нулю, если числитель равен нулю
Заданному промежутку [ 0; 5] принадлежит х =4.
Найдем значение функции на концах промежутка и в точке х =4 .
Сравним найденные значения и получим, что наибольшее значение функции равно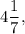 а наименьшее значение функции равно
а наименьшее значение функции равно 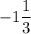
#SPJ1