1. Алгебра
  2. ЗНАТОКИ ХЕЛП найдите интервалы

ЗНАТОКИ ХЕЛП найдите интервалы возрастания и убывания функции y=f(x), когда
2.Найдите экстремумы функции y=f(x), когда

​


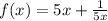
f(x) = 5x + \frac{1}{5x}
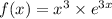
f(x) = x {}^{3} \times e {}^{3x}

vladislav4239 vladislav4239    3   28.01.2021 11:44    2

Ответы
Charafoxcoteyca34 Charafoxcoteyca34  27.02.2021 12:06

1)

\displaystyle f(x)=5x+\frac{1}{5x}=\frac{25x^2+1}{5x}\\\\f`(x)=\frac{25*2x*5x-5*(25x^2+1)}{25x^2}=\frac{25*10x^2-25*5x^2-5}{25x^2}=\frac{5(50x^2-25x^2-1)}{25x^2}=\\\\=\frac{25x^2-1}{5x^2}\\\\f`(x)=0\\\\25x^2-1=0; x^2=\frac{1}{25}; x=\pm \frac{1}{5}\\\\x\neq 0

__+____ -1/5__-___0___-__1/5___+_

возрастает        убывает              возрастает

(-оо; -1/5]            [-1/5;+1/5]                 [1/5;+oo)

2)

\displaystyle f(x)=x^3*e^{3x}\\\\f`(x)=3x^2*e^{3x}+e^{3x}*3*x^3=e^{3x}*3x^2(1+x)\\\\f`(x)=0\\\\x=0; x=-1

__-_____ -1__+___0__+___

 убывает     возрастает

х= -1 точка  минимума

х=0 точка перегиба

       

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
TaKuRGRAF TaKuRGRAF  14.01.2021 20:09
2+2+2+2++2+2+2+2+2++2+2+2+2+2+2+2+2++2+2++2+2+++22+2+++2+2+2+2+2+2++2+2+2+2+2++2+2+2++2+2+2+2++2+2+2...
Igrilla19990 Igrilla19990  14.01.2021 20:09
Разложить многочлен на множитеои​...
853692 853692  14.01.2021 20:08
Докажите тождество √a²b=/a/×√b​...
VETALmc005 VETALmc005  14.01.2021 20:08
Сколько будет 2 плюс 2 умножить на 2 сколько получится по идее 8 если я не прав исправте...
Красотка1000485 Красотка1000485  14.01.2021 20:08
Переобразуйте много член в:с²-0‚7с³)²г:(4у³-0‚5у²)²е:(0‚6b-60b²)²а: (а²-3а)²б:(1/2х³+6х)²...
камила905 камила905  14.01.2021 20:08
Чяяядтолфябью фтоцдалжЙД отвдцсцдцльты тдлысцдлшжадф...
никанана никанана  14.01.2021 20:07
Https://i.imgur.com/bijnljl.png...
Taylis69 Taylis69  19.06.2019 07:30
Вкакую степень нужно возвести число 4,чтобы получить 20...
089280ig 089280ig  05.05.2020 01:00
Решить неравенства:1) log₃(x^2-1)2)log²₀,₅x-log₀,₅x 33) log₂ 5-x/x-8 + log₀,₅(x-5) =log¹/₂(x-8)^2...
karina809 karina809  05.05.2020 01:18
Скільки ударів виконає годинник за добу, якщо кожну годину він відбиває кількість ударів, що дорівнює цифpі на годиннику?​...

Популярные вопросы