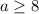Желательно расписать принцип и объяснения. при каком значении а область определения функции f(x)= (корень: -x^2+2x+a) + (корень: x-4). является одна точка
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. у человека ген длинных ресниц доминирует над геном коротких ресниц. женщина с...
1 - Начертить прямой угол. обозначить его вершину буквой а. на одной стороне угла отложить...
3 - Входе революции были устранены мешавшие развитию франции препятствия. (несколько...
3 - Дописать реакции 1) hcl+naoh= 2) hno3+lioh= 3)h2so4+mg(oh)2=...
1 - Чему равен период собственных колебаний в контуре, если его индуктивность равна...
2 - Лыжник массой 60 кг скатывается с горы при этом за любые 3с его скорость увеличивается...
3 - Какова роль односоставных предложений?...
3 - Найдите высоту равностороннего треугольник со стороной a см закрытьчитайте также...
2 - Решите : y-семь двенадцатых y= 4 целых одна шестая; (3,1х+х): 0,8=2,05; решается...
1 - Что то не так в этом стихотворение. особенно 2 столбик 2 строка. исправить. стих...
2
Составим систему неравенств, описывающую область определния данной функции: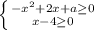
Второе неравенство системы равносильно неравенству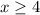 .
.
Для того, чтобы функция при нектором а имела бы в области определения единственную точку, необходимо, чтобы при этом значении а число 4 входило во множество решений неравенства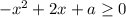 .
.
ответ: при