Здавствуйте обьясните как решать неравенство подобное етому

Ответы

Marattadjibov73 24.05.2020 05:53

Иррациональное неравенство.

Равносильно совокупности двух систем неравенств:

$\left[ {\begin{cases} x^2-1\geq0\\x\geq0\\(\sqrt{x^2-1})^2x^2 \end{cases} \\ \begin{cases} x^2-1\geq0\\x<0 \end{cases}}$

$\left[ {\begin{cases} (x-1)(x+1)\geq0\\x\geq0\\x^2-1x^2 \end{cases} \\ \begin{cases} (x-1)(x+1)\geq0\\x<0 \end{cases}}$

Первая система в данном случае не имеет решений, т.к. не имеет решений неравенство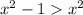 x^2-1x^2

$0\cdot x^21$

Во второй системе 1ое неравенство имеет решение х∈(-∞;-1]U[1;+∞), а 2ое - х∈(-∞;0), что в итоге дает х∈(-∞;-1]

$\begin{cases} \left[ {x\leq -1 \\ x\geq1} \\x<0 \end{cases}$

$\left[ {\begin{cases} x\leq -1 \\x<0 \end{cases} \\ \begin{cases} \\ x\geq1\\x<0 \end{cases}}$

(вторая система нет решений, первая - х∈(-∞;-1] "меньше меньшего")

ответ: х∈(-∞;-1]

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Dasha57891 11.05.2021 14:53

Gonsh1240 14.04.2020 09:26

dimidom56 14.04.2020 09:26

(3+c)(9-3c+c²) представить в виде многочлена...

artur17499 14.04.2020 09:26

WiTaMiN111 14.04.2020 09:26

miniahmetovtimu 14.04.2020 09:26

MelissaRacoon 14.04.2020 09:26

dianaandmasha 14.04.2020 09:27

geralump 14.04.2020 09:27

P−3,4=0,8 решите уравнение...

0KULLEP0 15.09.2019 17:10