Задана функция y=f(x), и два значения аргумента х1 и х2. требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа 3) сделать чертеж f(x)=12^(1/x) x1=0 x2=2
Другие вопросы по теме Алгебра
Популярные вопросы
- :одна сова съедает за лето 1000 мышей,которые питаются зерном. этому сохраняется...
3 - Какая масса соли образуется при взаимодействии 10 моль соляной кислоты с гидроксидом...
3 - Напишите небольшое сочинение по языку на тему (или просто можно придумать) как...
2 - Длинна участка земли прямоугольной формы 44 м а ширина на 24 м меньше . десятою...
2 - За одну открытку нужно заплатить 5 р.сколько таких открыток можно купить на 15...
2 - Какова масса углекислого газа взятогов количестве 0,5 моль...
2 - Окружающий мир 1 класс планета знаний составить режим дня...
2 - Слова длинной 8 символов все слова начинаются с а.о.б.к. остальные могут быть...
2 - Наталя записала дріб, різниця знаменника і чисельника якого дорівнює 15. після...
2 - 28. а) спишите, расставив знаки препинания.после н..ч..ных зам..ро..ков ре..ко...
3
Функция f(x) неопределена в точке x=0 и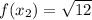 . Следовательно, в точке
. Следовательно, в точке 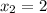 разрыва нет, а в точке
разрыва нет, а в точке 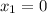 - точка разрыва.
- точка разрыва.
Точка х=0 не принадлежит области определения функции, то при х=0 функция имеет точку разрыва второго рода.
Для построения функции посчитаем предел