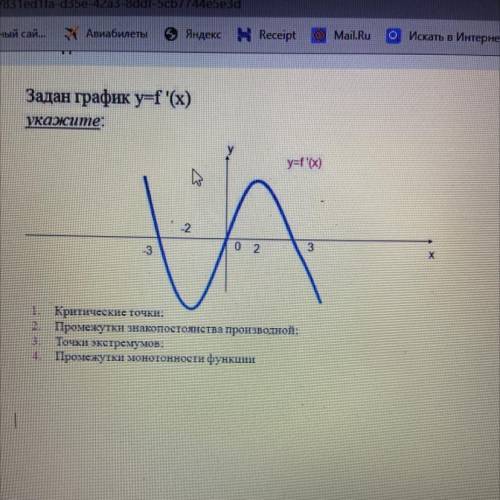
Задан график y=f(x) укажите:
у
y=f'(х)
-2
02
3
-3
X
1. Критические точки:
2. Промежутки знакопостоянства производной:
3.
Точки экстремумов:
4. Промежутки монотонности функции

Чтобы ответить на данный вопрос, рассмотрим график функции и определим искомые характеристики по осям Ox и Oy.

1. Критические точки:
Критические точки - это точки, в которых производная функции равна нулю или не существует. На графике можно заметить, что в точках x = -2, x = 0, x = 2 и x = 3 происходят изменения направления склона функции. Значит, эти точки являются критическими точками.

2. Промежутки знакопостоянства производной:
Для определения промежутков знакопостоянства производной, нам необходимо изучить участки графика, где производная положительна (выше оси Oy) или отрицательна (ниже оси Oy). На графике можно заметить, что производная положительна на интервалах (-∞, -2) и (0, 3), а отрицательна на интервалах (-2, 0) и (3, +∞).

3. Точки экстремумов:
Точкой экстремума является точка, в которой происходит изменение направления склона функции. Из графика видно, что в точках x = -2 и x = 2 происходит смена направления склона функции, значит, в этих точках находятся экстремумы.

4. Промежутки монотонности функции:
Для определения промежутков монотонности функции нам необходимо изучить знак производной на каждом участке графика. Из графика можно сделать вывод, что функция возрастает на интервалах (-∞, -2) и (2, 3), и убывает на интервале (-2, 2).

Таким образом, ответ на вопрос будет следующим:
1. Критические точки: x = -2, x = 0, x = 2, x = 3.
2. Промежутки знакопостоянства производной: (-∞, -2), (-2, 0), (0, 3), (3, +∞).
3. Точки экстремумов: x = -2, x = 2.
4. Промежутки монотонности функции: (-∞, -2), (-2, 2), (2, 3).