Якщо довжину прямокутника зменшити на 3 см, а ширину збільшити на 2 см, то його площа збільшитсья на 6 см квадратних. Якщо довжину прямокутника зменшити на 5 см, а ширину збільшити на 3 см, то площа прямокутника не зміниться. Знайдіть сторони данного прямокутника
Другие вопросы по теме Алгебра
Популярные вопросы
- Раскрой скобки и упрости выражение: −8(4−a)+3(−2a−2)−6(−9+a). ответ: выражение...
1 - 8. The girl ... him. Select the right answer.kissingkisseskiss...
2 - Найти экстремумы функции: 1) f(x)=-x^3+x^2 решить...
3 - Дан равнобедренный треугольник abc основание ac равно 4 корня из 2 см медиана ам=...
3 - Zn → FeSO4 → X → ZnO осуществить цепочку...
1 - Складіть назви за систематичною номенклатурою...
2 - Якій алгоритмічній конструкції відповідає зображена на малюнку блок схема...
3 - Со словом в котором корень суффикс (к) и окончание (а)...
1 - с геометрией Даны числа a, b и c, причем 0 a b c и a,b и c – стороны прямоугольного...
3 - Які заходи з охорони води нині існують та впроваджуються?...
2
Нехай см — довжина прямокутника, а
см — довжина прямокутника, а 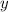 см — його ширина. Площа
см — його ширина. Площа 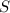 прямокутника дорівнює добутку довжини
прямокутника дорівнює добутку довжини
Якщо довжину прямокутника зменшити на 3 см, а ширину збільшити на 2 см, то його площа збільшитсья на 6 см квадратних. Отже,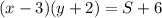 , а саме
, а саме 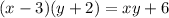 .
.
Якщо довжину прямокутника зменшити на 5 см, а ширину збільшити на 3 см, то площа прямокутника не зміниться. Отже,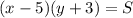 , а саме
, а саме 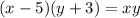 .
.
Маємо систему з двох рівнянь з двома невідомими:
Розв'яжимо цю систему методом додавання:
Додамо почленно обидва рівняння. Отримаємо рівняння зі зімнною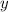 :
:
Тоді
Отже, довжина прямокутника дорівнює 15 см, а ширина — 6 см.
Відповідь: 15 см; 6 см.