X^2-2ax +a+20=0 при каких значениях а уравненние имеет корни?
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько надо взять серы, чтобы при взаимодействии ее с железом получилось...
3 - Ещё заполните пропуски предлогами времени 1.come … five o’clock....
3 - Гоша измерил треугольника. сумма длин первой и второй стороны ровна...
3 - Выяснить какими звуками различаются в произношении слова завет и...
1 - Во время злости или страха сосуды кожи расширяются и увеличиваются...
2 - Решить примеры двумя любыми см + 13 м 48 дм 9 см 4876 кг + 9 т 5...
1 - Докажите,что . положение материка оказывает влияние на его природу...
1 - Переведите в этот день мой будильник не звонит.я остаюсь в постели...
3 - Найдите значение выражения 1,78: 1,4*0,7...
3 - Какие были сходства у князя олега и игоря в правлении?...
3
x^2-2ax+a+20=0
1) a=0, x^2+20=0 - нет решений ;
2) a#0, D=4a^2-4(a+20)=4a^2-4a-80=4(a^2-a-20)
D=0, то a^2-a-20=0
a1=-4, a2=5
Если а=-4, то х=а=-4
Если а=5, то х=а=5
D<0, то аЄ(-4; 5) - уравнение не имеет решений
D>0, то аЄ(- бесконечность; -4)U(5; + бесконечность)
x1=(2a-2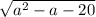 )/2=a-
)/2=a-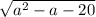
x2=a+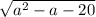
Уравнение имеет решения при аЄ(- бесконечность; -4]U[5; + бесконечность)
Уравнение имеет корни, если дискриминант не отрицателен.
D = 4a²- 4(a+20) >=0
a²- a - 20 = 0 найдем корни
а1 = 5
а2 = -4
D = (a-5)(a+4)>=0
дискриминант положителен, когда обе скобки имею один знак, т.е.
а<=-4 и а>=5
ответ: уравнение имеет корни при а ∈ (-∞;-4]U[5;∞)