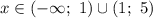(x-1)^2(x-5)< 0 подробно решите неравенство
Другие вопросы по теме Алгебра
Популярные вопросы
- Алгебра... кто умный это 8 класс...
1 - Выполните действие:(17 5/14-29 4/21)*(32,098+5,902)/49 1/7-30 10...
3 - S=0,7 a=10m/s2 t=0,2min v-?...
2 - 7 тапсырма . Казахский язык...
1 - Які координати має точка, симетрична точці C(-2; 6) сно точки O(3; 4)?...
2 - , подскажите по Казахскому...
2 - написать проект про дом будущего...
1 - Робот – это автоматизированное , созданное по принципу живого организма. Датчик...
3 - Какое число в натуральном ряду следует за числом 45...
1 - 1.Зат есімнің сұрағын көрсетіңіз? А. Не істеді? Қайтті?В.Кім? Не ?С. Неше? Нешеу?...
3
Первый
Анализируем: здесь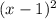 — неотрицательная величина; имеем: при умножении неотрицательной величины с другим выражением мы можем получить отрицательное число, если второе выражение будет отрицательным, а первое — не равным нулю:
— неотрицательная величина; имеем: при умножении неотрицательной величины с другим выражением мы можем получить отрицательное число, если второе выражение будет отрицательным, а первое — не равным нулю:
Итак, общим ответом будет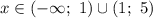
Второй
Решим неравенство методом интервалов:
1) Найдем нули данного выражения:
2) ОДЗ: все числа
3) Начертим координатную прямую и отметим нули данного выражения выколотыми точками (так как неравенство строгое) и определим знак на каждом участке и объединим участок (участки), содержащие знак "минус" (см. вложение).
Итак, общим ответом будет