1. Алгебра
  2. Высота, проведённая из вершины

Высота, проведённая из вершины прямого угла, равна 2 см и делит гипотенузу на отрезки, один из которых больше другого на 3 см. Найдите стороны треугольника.

sudarev2018 sudarev2018    3   05.07.2021 10:19    1

Ответы
ttmail95 ttmail95  04.08.2021 10:40

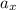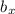Так как высота проведена из вершины прямого угла то высота попадет на гипотенузу.  А отрезки на которые делит высота гипотенузу являются проекциями катетов пусть  с-это гипотенуза  ; \displaystyle\ a_x  и   \displaystyle\ b_x   -это проекции катетов(сторон треугольников) a и b ;  для них есть правила  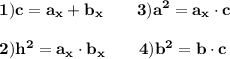                                                                                           \displaystyle\bf 1)c=a_x+b_x\qquad 3)a^2=a_x\cdot c\\\\2)h^2=a_x\cdot b_x \qquad 4)b^2=b\cdot c                                                                              нам известно    что  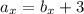 \displaystyle\ a_x=b_x+3     дальше будем использовать 2-ю формулу  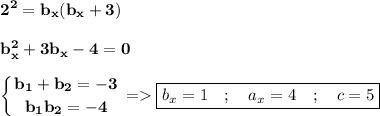                                                                                               \displaystyle\bf 2^2=b_x(b_x+3)\\\\b_x^2+3b_x-4=0 \\\\\left \{ {{b_1+b_2=-3} \atop {b_1b_2=-4}} \right. =\boxed{b_x=1\quad ; \quad a_x=4\quad ; \quad c=5}                                             Дальше найдем стороны a и b через 3-ю и 4-ю формулу  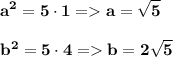                     \displaystyle\bf a^2=5\cdot1= a=\sqrt{5} \\\\b^2=5\cdot4= b=2\sqrt{5}                                                                                       ответ: у треугольника длины сторон равны   √5 ; 2√5  и 5                                                                                                                                                                                                        


Высота, проведённая из вершины прямого угла, равна 2 см и делит гипотенузу на отрезки, один из котор
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
moiseenkova041 moiseenkova041  12.12.2020 21:44
заранее желательно ответить на все задания​...
NikolayNik12 NikolayNik12  12.12.2020 21:53
решить с подробным объяснением....
optymus optymus  16.05.2020 22:08
Розкласти многочлен на множники 9а -9а зробіть правильно і бистріше будь ласка ів та ще й підпишуся !​...
Yuliaddd Yuliaddd  16.05.2020 22:08
Кубом какого одночлена является одночлен 0,027x^30 y^6 z^12?​...
Snyezha Snyezha  16.05.2020 22:08
ДАМ ЛУЧШИЙ ОТВЕТ Катер проплив 4 км проти течії і 15 км за течією річки за той самий час, який йому знадобився для проходження 18 км озером. Яка власна швидкість катера, якщо швидкість...
uylia144348 uylia144348  06.05.2021 12:55
Вкажи пару чисел , що є розв язком рівняння 2x-y=41. Відповідь: (0;41) (2;0) (-1;41) (0;-41) (1;2)...
сергей1106 сергей1106  06.05.2021 12:54
980. Оцените относительную погрешность приближенного значения плотности p (в г/см*), взятого из справочника, если:в) px 5,20 - 103;д) px 1,7-10-2;б) px 9,12 - 10; г) px 6,0. 102;...
Kurtizan Kurtizan  06.05.2021 12:54
ХЛП а) (|х| − 2N) 2 + (у − 0,5х) 2 = 0 б)Теплохід проходить відстань між пристанями в одному напрямі за N год, а в протилежному – за (N + 1) год, а за 2 год за течією річки і за...
bdhdt bdhdt  06.05.2021 12:53
{1,2х-2,5у=4 {-1,4х+1,5у=1{-1,4х+1,5у=1 Математика 6-класс ​...
funfup funfup  26.09.2019 20:30
Знайти область визначнои функции коринь 21+31х 7коринь 16х2+18...

Популярные вопросы