1. Алгебра
  2. Выражение ( sin a/2 + cos

Выражение ( sin a/2 + cos a/2)^2/ 1+sina найдите угловой коефицент касательной, проведенной к графику функции f(x)=2-x^2+3x^4 в точке с абсцисой x0= -2 точка движется по координатной прямой согласно закону x(t) = 4t^2 где x(t)-координата точки в момент времени t. найдите скорость точки при t=2.

rufinafin rufinafin    1   22.05.2019 11:30    0

Ответы
ZA25 ZA25  01.10.2020 07:04

\displaystyle \frac{(\sin \frac{\alpha}{2}+\cos\frac{\alpha}{2})^2}{1+\sin\alpha}=\frac{\sin^2\frac{\alpha}{2}+2\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}+\cos^2\frac{\alpha}{2}}{1+\sin\alpha}=\frac{1+\sin\alpha}{1+\sin \alpha}=1

Здесь было использовано основное тригонометрическое тождество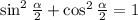 \sin^2\frac{\alpha}{2}+\cos^2\frac{\alpha}{2}=1 и использована формула синуса двойного угла: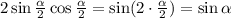 2\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}=\sin(2\cdot\frac{\alpha}{2})=\sin\alpha


2) По геометрическому смыслу производной: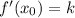 f'(x_0)=k, т.е. производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

f'(x)=(2-x^2+3x^4)'=12x^3-2x\\ k=f'(-2)=12\cdot(-2)^3-2\cdot(-2)=-92


ответ: -92.


3) По физическому смыслу производной: v(t) = x'(t).

x'(t)=(4t^2)'=8t\\ v(2)=8\cdot2=16


ответ: 16 м/с.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
shlama283 shlama283  25.12.2021 05:49
5. Решите графическим методом систему уравнений и найдите координаты точки пересечения графиков функций: y = 6x - 1 х- у = -4...
mariaalimardonova mariaalimardonova  25.12.2021 05:40
Пропорции лица ПРОПОРЦИИ ЛИЦА Задание 1/2 У большинства взрослых людей с правильными (симметричными) пропорциями лица промежуток между глазами, считая между их внутренними углами,...
vadim2556 vadim2556  25.12.2021 05:39
Школьникам предлагалось разгадать несколько числовых закономерностей и вписать в пропуски недостающие числа. оценка осуществлялась по количеству правильно решенных задач и дала...
seregasasaas seregasasaas  25.12.2021 05:35
43. Постройте график функций у 2 и вставьте пропушение слова в следумовою х 2 предложение: «Функция вида у - называется ее графиком является ее ветви расположены в так как значение...
KIrito5016 KIrito5016  25.12.2021 05:32
Найдите разность арифметической прогрессии S40 в которой b1=4, d=1...
graulity graulity  16.09.2019 06:30
Loga(ab^2), если logb a=2/11 решите...
nalimovshurik nalimovshurik  16.09.2019 06:30
А–7 кр–5 «одночлены и многочлены» вариант 3 1. выражение: а) (6a2 – 3a + 8) – (2a2 – 5); б) 3x4 (7x – x5). 2. решите уравнение 14 + 4(5х – 2) = 44х – 30. 3. вынесите общий множитель...
Viki3888 Viki3888  16.09.2019 06:30
Sinx=0. позначити на тригонометричному колі...
ashueva1919 ashueva1919  16.09.2019 06:30
Вынесите общий множитель за скобки: 1.a(3b+c)-x(3b+с) 2. 2p(a--a) 3. 3(a-2)^2-3(2-a)...
Динара22235 Динара22235  16.09.2019 06:30
Последовательность (an) задана формулой an=2,5n+2. найдите сумму членов последовательности с одиннадцатого по двадцатый включительно...

Популярные вопросы