Выполнить задание с двойным неравенством,
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите программу, в которой объявляется массив размером 5х10...
2 - Средняя плотность населения наибольшая … 1) в Египте 2) в Японии...
2 - Как оформить читательский дневник Два Ивана-солдатских сына?...
2 - Для какого наболее целого значения А выражение (6y-2x A) + (y x)...
1 - у трикутнику ABC проведено медіану CM. на на стороні BC відмічено...
1 - Найдите сумму квадратов корней уравнения 4х²-7х-1=0...
3 - Какую наименьшею силу следует приложить к стальному бруску, находящемуся...
2 - Постройте равнобедренный треугольник по боковой стороне и высоте,...
1 - за задачу по экономике, сама не могу разобраться(( Пусть технологии...
1 - Найдите сумму квадратов корней уравнения 4х²-9х-1=0...
2
Запишем в виде системы двойное неравенство.
(3х-1)/(2х+1)>1
(3х-1)/(2х+1)<2
Решим одно неравенство системы, потом другое, а потом пересечем ответы для нахождения решения исходного неравенства.
(3х-1)/(2х+1)>1; ((3х-1)-(2х+1))/(2х+1)>0;(х-2)/(2х+1)>0, решаем методом интервалов.
-0.52
+ - +
Решением будет объединение интервалов (-∞;-0.5)∪(2;+∞)
Решим второе неравенство. (3х-1)/(2х+1)<2
((3х-1)-2*(2х+1))/(2х+1)<0; (3х-1-4х-2)/(2х+1)<0; (-х-3)/(2х+1)<0; (х+3)/(2х+1)>0; опять решим методом интервалов
-3-0.5
+ - +
Решением будет объединение интервалов (-∞;-3)∪(-0.5;+∞)
Пересечением этих двух ответов является общее решение (-∞;-3)∪(2;+∞), нас интересуют все целые значения х, для которых неравенство не выполняется, т.е. [-3;2], в область определения не входило значение х=-0.5, но оно не является целым, итак, все целые такие -3; -2; -1; 0; 1; 2.
ОДЗ: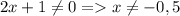
Данное двойное неравенство представим в виде системы неравенств:
1) Решим первое неравенство: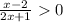
+ - +
_______-0,5__ __ __ __ __ ___2______
(-∞; -0,5)∪(2; +∞)
2) Решим первое неравенство: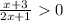
+ - +
_______-3___ ___ __ __ __ ___ __-0,5___________
(-∞; -3)∪(-0,5; +∞)
3) Общее решение системы
________-3__ __ ___ ___ ___ ___2______________
(-∞; -3)∪(2; +∞) - это промежутки, где неравенство выполняется.
4) Очевидно, что данное неравенство НЕ выполняется на промежутке
[-3; 2].
Перечислим целые значения из этого промежутка:
-3; -2; -1; 0; 1; 2 (это и есть ответ).