Алгебра: Найдите сумму квадратов корней уравнения 4х²-9х-1=0

Найдите сумму квадратов корней уравнения 4х²-9х-1=0

Ответы

настя7322 15.10.2020 15:28

По теореме Виета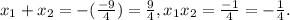 $x_1+x_2=-(\frac{-9}{4})=\frac{9}{4}, x_1x_2=\frac{-1}{4}=-\frac{1}{4}.$

Так как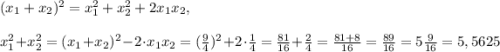 $(x_1+x_2)^2=x_1^2+x_2^2+2x_1x_2, \\\\x_1^2+x_2^2=(x_1+x_2)^2-2\cdot x_1x_2=(\frac{9}{4})^2+2\cdot\frac{1}{4}=\frac{81}{16}+\frac{2}{4}=\frac{81+8}{16}=\frac{89}{16}=5\frac{9}{16}=5,5625$

ПОКАЗАТЬ ОТВЕТЫ

TOkenov 15.10.2020 15:28

4x² - 9x - 1 = 0

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = (-9)² - 4·4·(-1) = 81 + 16 = 97

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x₁ =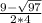 $\frac{9-\sqrt{97} }{2*4}$ ≈ -0.10611

x₂ =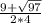 $\frac{9+\sqrt{97} }{2*4}$ ≈ 2.3561

ответ: х₁≈ -0.10611; x₂ ≈ 2.3561

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

saya8282 15.11.2019 09:49

(1/5)^x =1/25 розв яжіть нерівність...

fedosovsemen 15.11.2019 09:54

перший хостел розраховано на m осіб а другий на n осіб (n m). першый хостел плануэться розширити на x місць щоб усього місць в хостелі стало в 4 рази більше ніж у другому вкажіть...

Jamal20 30.08.2019 09:40

Разложите на множители данные выражения: ax²-4a 3m²-12m+12 5x³+5y³ z⁴-x^12...

timon040805 30.08.2019 09:40

Решите неравенство (x^4 + 4*x^2 - 5)/(x^2 + 5*x - 6) = 0...

skyblue1 30.08.2019 09:40

Решите уравнение (2x-1/14x^2+7x)+(8/12x^2-3)=(2x+1/6x^2-3x)...

nnnnnastasi 30.08.2019 09:40

Все свои ! запишите данные многочлены как сумму двучленов и разность двучленов xy-xz-y-z ab-b+ac-c ax в степени 2 +x+a+1...

dorof077 30.08.2019 09:40

Решите неравенства 1) х-8/11+х 0 2) 13+х/2,5х 0 3) х+7/3-х 0 4) 2х-4/х+2 0 решите все и подробно с чертижом решите до 11: 00 или 12: 00...

Leoapps 08.05.2020 20:19

Берілген қабырғасы және оған іргелес жатқан бұрыштары бойынша үшбұрыш салыңдар AB=5см, A=35 градус .B=65градус. көмек беріріңіздерші. ...

DmitryKind98 08.05.2020 20:20

5. Чисельник дробу на одиницю менший від знаменника.Якщо чисельник дробу збільшити на 2, а знаменник зали-шити без змін, до дістанемо дріб, на одиницю більший відпочаткового....

kote03012 08.05.2020 20:20

У многочлен и найди его числовое значение: −cbc+c2b2cb+4,4, если c=2, b=1,3....

Найдите сумму квадратов корней уравнения 4х²-9х-1=0​

Популярные вопросы

Найдите сумму квадратов корней уравнения 4х²-9х-1=0