Вычислите значения тригонометрических, если 
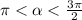
Другие вопросы по теме Алгебра
Популярные вопросы
- Https://www.mevue.com/watch/7aPb16hHefWbAQN https://www.mevue.com/watch/vi2RrLFClLklylN...
1 - Запишите в десятичной системе число, которое в двоичной системе записано так: 100100111...
2 - Определите поперечное увеличение, даваемое симметричной двояковыпуклой линзой с...
1 - Всех девочек с 8 мартом Посмотрите историю , всего 2 задания . Благодарю...
1 - В чем заключались главные особенности экономического развития России во второй...
2 - В 6-м предложении Найди слово, состав которого соответствует схеме: коронень, суффикс,...
1 - этим веществам нужно добавить Fe₂O₃ Начертите в тетради предлагаемую таблицу. В...
1 - Определи степень данного многочлена, ответ запиши словами. ВСЁ СМОТРЕТЬ НА ФОТО...
2 - На координатной прямой отмечены точки A, B и C. Установите соответствие между точками...
2 - ПАМОГИТЕ ДАМ 35 3 ЗАДАНИЕ СДЕЛАИТЕ Read these sentences and choose have to, has...
3
Основное тригонометрическое тождество: .
.
Выразим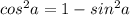 .
.