Вычислите. sin2α, cos2α, tg2α ,если: а)sinα=-3/5 и π
Другие вопросы по теме Алгебра
Популярные вопросы
- Техническая механика. Нужно ответить на вопросы:1)Для чего предназначены...
2 - Решите уравнение:а) х2+5х2-6=0b) 2x2-3х +6=0...
3 - Найди значение логического выражения: F=(0^0)(1v1) Я всё сделаю для...
2 - Вершины треугольника АВС имеют координаты А(-1;-5), В(-5;-8), С(-7;-13)....
2 - Считаете ли вы, что в нашем мире существуют экологические проблемы?...
2 - Алгоритм позбавлення шкільної звички...
1 - Как выйти из семьи в гта самп...
3 - Все показано на картинках ниже!...
2 - Приведите любой пример использования знаний о строении цветковых растений...
3 - В чём заключалась задача Жульена в доме Реналей ?...
3
а)
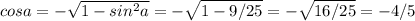
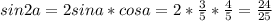
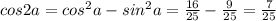
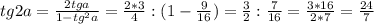
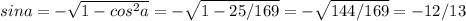
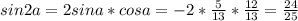
sina = -3/5
tga = sina/cosa = 3/5 : 4/5 = 3/4
б)
cosa = 5/13
tga = sina/cosa = -12/13 : 5/13 = -12/5
в)