Вычислите площадь фигуры заключенной между следующими линиями: a) осями координат, прямой х=5 и кривой y=2x^2-5 b) пораболой y=5x^2-2x и осью ox

Ответы

happynik20021 27.05.2020 11:48

а) Наудем точку пересечения кривой с осью х:

2 $2x^{2}-5=0\\ x^{2}=2,5\\ x=\± \ \frac{\sqrt{10}}{2}$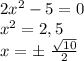

Площадь фигуры между линиями равна определенному интегралу в интервале значений х, а подинтегральном выражении разность функции(функция выше минус функция ниже).

Получаем сумму двух интегралов:

$\int\limits^\frac{\sqrt{10}}{2}_0 {0-(2x^{2}-5)} \, dx+ \int\limits^5_\frac{\sqrt{10}}{2}} {2x^{2}-5} \, dx$

$\int\limits^\frac{\sqrt{10}}{2}_0 {0-(2x^{2}-5)} \, dx= \int\limits^\frac{\sqrt{10}}{2}_0 {5-2x^{2}} \, dx=5x-\frac{2x^{3}}{3}|\limits^\frac{\sqrt{10}}{2}_0=\\=\frac{5\sqrt{10}}{2}-\frac{20\sqrt{10}}{24}=\frac{40\sqrt{10}}{24}=\frac{5\sqrt{10}}{3}$

$\int\limits^5_\frac{\sqrt{10}}{2}} {2x^{2}-5} \, dx = (\frac{2x^{3}}{3}-5x)|\limits^5_\frac{\sqrt{10}}{2}}=\frac{250}{3}-25-\frac{20\sqrt{10}}{3}+\frac{5\sqrt{10}}{2} =\\=\frac{5\sqrt{10}}{3} +\frac{175}{3}$

Складываем:

$\frac{5\sqrt{10}}{3} +\frac{175}{3} +\frac{5\sqrt{10}}{3} = \frac{10\sqrt{10}+175}{3}$

б) находим точки пересечения с осью y

$5x^{2}-2x=0\\ x(5x-2)=0\\ x = 0 \ \ \ \ \ 5x=2\\ / \ \ \ \ \ \ \ \ \ \ \ \ x = 0,4$

Получаем интеграл:

$\int\limits^\frac{2}{5}_0 {0 -(5x^{2}-2x)} \, dx = (x^{2}-\frac{5x^{3}}{3})|\limits^\frac{2}{5}_0=\frac{16}{100}-\frac{32}{300}=\frac{16}{300}=\frac{4}{75}$