Вычислите arcsin ( cos (2arcctg (под корнем (2)-
Ответы
Пусть угол ![\alpha\in(0,\frac\pi2]](/tpl/images/0173/6659/99927.png) таков, что
таков, что 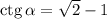 . Найдём
. Найдём 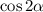 .
.
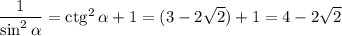
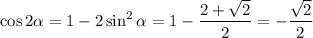
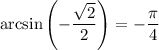
ПОКАЗАТЬ ОТВЕТЫ
![\alpha\in(0,\frac\pi2]](/tpl/images/0173/6659/99927.png) таков, что
таков, что 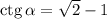 . Найдём
. Найдём 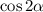 .
.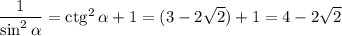
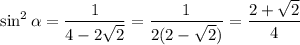
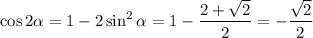
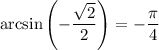
Другие вопросы по теме Алгебра
Популярные вопросы
- Енді біреуі менімен тұстас болуы керек,ақшыл денелі арық,бір...
3 - Поэма У самого моря во Где происходит действие поэмы?2 Определите...
1 - Що вкрав павлуша в школі?...
1 - Каковы были условия мира, заключённого Октавианом Августом с...
2 - До ть розв язати це рівняння...
1 - Заполни таблицу реальные союытия в произведении сказочные (фольколорные)моменты(минимум...
2 - Среди предложений 7-10 найдите такое(-ие), которое(-ые) связано(-ы)...
3 - 1.Где происходят события поэмы М.Ю.Лермонтова «Мцыри»? Грузия....
3 - Найти мощность тока если напряжение равно 0.02 кВ сопротивление...
3 - А) Екі жұмысшы бірге 90 000 тг еңбекақы алды. Бірінші жұмыс-шы...
3