Вычислите 8 класс (на фото
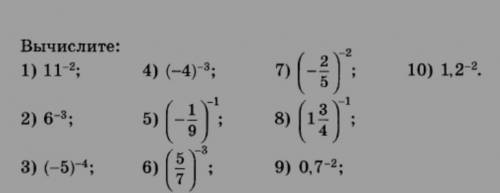
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинение на тему герой нашего времени о михаи́л серге́евич...
3 - Напишите краткий пересказ по теме голосемянные растения биология...
3 - Как определить у слов инфинитивов ощутить, полюбить, проникнешь,...
2 - Апiшiце кветку, якая падабаецца вам больш за iншыя.складзены...
3 - This is our living room.it s big and beautiful.there are many...
2 - Мне нужно стихотворение о светофоре на казахском...
1 - Сочините четверостишие или стих про тишину....
3 - Разберите глаголы как часть речи. не терпит не забывает прекращает...
3 - Длина отрезка равна 2 целым 3/4 см, а другого в 3 раза больше....
3 - Два самосвала перевозили цемент первый самосвал сделал 16 рейсов...
3
Формула вида y = mx + b, где m - это наклон, а b - это смещение.
Для начала, давайте определим наклон прямой, проходящей через точки A (9, 8) и B (12,14).
Наклон (m) можно найти, используя формулу:
m = (y2 - y1) / (x2 - x1)
где (x1, y1) это координаты точки A, а (x2, y2) это координаты точки B. Подставляя значения:
m = (14 - 8) / (12 - 9)
m = 6 / 3
m = 2
Таким образом, наклон прямой, проходящей через точки A и B, равен 2.
Теперь нам нужно используя эту информацию, чтобы найти уравнение прямой, проходящей через точку C (8, y). Мы можем использовать наклон (m) и координаты точки C в формуле y = mx + b, чтобы найти смещение (b).
У нас есть уравнение y = mx + b, где y = y-координата точки C (неизвестная), x = x-координата точки C (известная), m = 2 (наклон, которым мы только что опеределили).
Подставляя значения:
8 = 2 * 8 + b
Решим уравнение для b:
8 = 16 + b
b = 8 - 16
b = -8
Таким образом, смещение (b) равно -8.
Теперь, используя полученные значения наклона (m) и смещения (b), мы можем записать уравнение прямой, проходящей через точки A и B:
y = 2x - 8
Таким образом, уравнение прямой, проходящей через точки A (9, 8) и B (12, 14), будет y = 2x - 8.
Теперь, чтобы найти значения x и y для 8-й параллели, мы можем использовать уравнение прямой, которое мы только что нашли. Подставляя x = 8 в это уравнение:
y = 2 * 8 - 8
y = 16 - 8
y = 8
Таким образом, x-координата для 8-й параллели равна 8, а y-координата равна 8.
Ответ: 8 класс (8, 8).