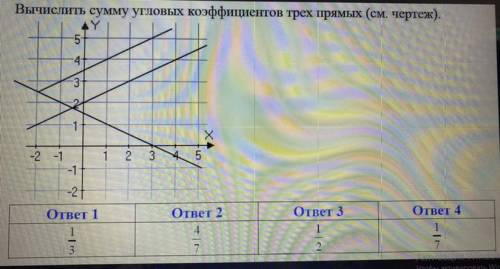
Вычислить сумму угловых коэффициентов трёх прямых

Хорошо, давайте разберем этот вопрос.

Для начала, нам нужно понять, что такое угловой коэффициент прямой. Угловой коэффициент (или коэффициент наклона) прямой показывает, насколько быстро или медленно прямая поворачивается при движении по оси x.

Угловой коэффициент прямой можно найти, сравнивая разницу между координатами двух точек на прямой. Для вычисления углового коэффициента, мы используем формулу:

m = (у2 - у1) / (х2 - х1),

где m - угловой коэффициент, (х1, у1) и (х2, у2) - координаты двух точек на прямой.

Теперь, давайте вернемся к нашему изображению и вычислим угловые коэффициенты для каждой из трех прямых.

1) Прямая AB:
У нас есть две точки на этой прямой: A(0,0) и B(3,5).
Подставим координаты в нашу формулу:
mAB = (5 - 0) / (3 - 0) = 5 / 3.

Таким образом, угловой коэффициент прямой AB равен 5/3.

2) Прямая BC:
У нас есть две точки на этой прямой: B(3,5) и C(6,0).
Подставим координаты в нашу формулу:
mBC = (0 - 5) / (6 - 3) = -5 / 3.

Таким образом, угловой коэффициент прямой BC равен -5/3.

3) Прямая AC:
У нас есть две точки на этой прямой: A(0,0) и C(6,0).
Подставим координаты в нашу формулу:
mAC = (0 - 0) / (6 - 0) = 0.

Таким образом, угловой коэффициент прямой AC равен 0.

Теперь, чтобы найти сумму угловых коэффициентов трех прямых, мы просто складываем их:
mAB + mBC + mAC = (5/3) + (-5/3) + 0 = 0.

Итак, сумма угловых коэффициентов трех прямых равна 0.

Пересчитав координаты на графике, можно заметить, что все три прямые пересекаются в одной точке, что объясняет, почему сумма их угловых коэффициентов равна нулю. Центр масс трех прямых лежит в этой точке.

Я надеюсь, что я смог дать вам подробное и понятное объяснение! Если у вас есть еще вопросы, не стесняйтесь задавать!