Вычислить интегралы: 1) 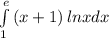
2) 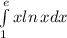
3) 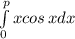
Другие вопросы по теме Алгебра
Популярные вопросы
- Заполните пропуск в тексте. Для этого наберите пропущенное слово на клавиатуре...
2 - Внутренняя политика Кыпчаков...
1 - Определите положительные и отрицательные последствия крестовых походов. И запишите...
3 - Task 3. Open the brackets putting the verbs into the Future Simple. 1) He__many...
2 - плз с казак адеб ТЖБ 1.«Ғылым таппай мақтанба» өлеңінің идеясына сай қатарды белгілеңіз....
3 - Какую роль играет музыка в исполнении эпоса?...
1 - Диагональ прямоугольника равна 10 см и образует с одной из его сторон угол 30°....
2 - 6.Какой прием используется в представленном ниже отрывке? «Теперь он стал весь...
1 - 8 сынып 2 тоқсан тжб ағылшын...
1 - Какие условия необходимы для того, чтобы рыночный механизм (взаимодействия спроса...
2
1.
По частям
2.
3.