Вычислить интеграл (заранее )
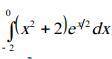
Другие вопросы по теме Алгебра
Популярные вопросы
- В арифметической прогрессии а12+а15=20.Найдите...
1 - 1. There is milk in the bottle. 2. Are there eggs in the recipe?...
3 - Плащадь трапеции изображённой на рисунке равна 728 основание...
2 - Немецкий. Прилагательные с неопределенным артиклем A) Adjektive...
2 - Звати прямокутні трикутники зображені на рисунку для кожного...
3 - На сторонах AB і BC трикутника ABC взято точки К і Р так, що...
1 - написать есе на тему Дружба між людьми і тваринами на основании...
2 - 11 клас до ть ) . Расписать как обычное решение...
3 - Можно ли не ходить в школу из за коронавируса в селе? ...
3 - Як вплинули реформи Петра І на розвиток Московського царства?...
1
Найдем неопределённый интеграл:
По частям:
Подставляем пределы: