Вычислить интеграл..............
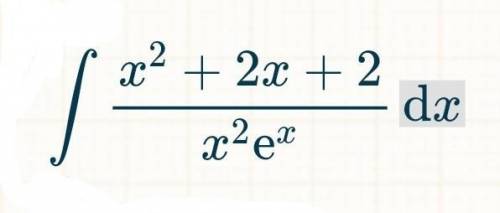
Другие вопросы по теме Алгебра
Популярные вопросы
- Унас 2 класс и не знаем как сделать окр.мир рассказ о редком растении или о...
2 - Решить по действиям -540: 9+(-450): 5+160=? и -860: 20-625: 25+75 решить по...
3 - 934*260 2468*359 1234*2007 столбиком и чтобы вверху были цифры как решили!...
1 - Выход растений на сушу связан с появлением в первую очередь 1 семян 2 цветков...
2 - Где обитают почвенные,молочнокислые,болезнетворные,азотофиксирующие бактерии?...
3 - Бөлгіш20,бөлінді7,қалдық18.бөлінгіш? а)188 б)178 в)148 с)158...
2 - 79: 4=? разделить с остатком.немогу решить. 3 класс...
3 - 20 ! придумайте сочинение на тему путешествие на поле славы (бородино)...
1 - Основные события 3 действия горе от ума...
2 - Цитати до хлопців грицька і санька з тексту джури козака швайки...
3
Второй интеграл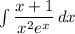 будем интегрировать по частям:
будем интегрировать по частям:
Интегрируем: