Вычислить двойной интеграл

Question

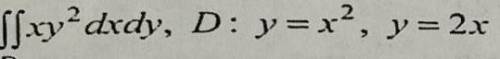
Алгебра: Вычислить двойной интеграл​

Evo4ka111 · Answer

Відповідь:6.4Пояснення:∫∫ху^2dxdy=∫_0^2 xdx ∫^(2x)_(x^2) y^2dy=∫_0^2 x(1/3y^3) |^(2x)_(x^2)dx=1/3∫_0^2 x(-x^6+8x^3)dx=1/3∫_0^2 (-x^7+8x^4)dx =1/3(-1/8x^8+8/5x^5)|_0^2=1/3(-1/8×2^8 +8/5×2^5)=1/3(-32+51.2)=1/3×19.2=6.4...

Вычислить двойной интеграл​

Популярные вопросы

Вычислить двойной интеграл