Всем доброго вечера : ) с дифференциальным уравнением. определить его тип и решить : ) !
Ответы
Уравнение Бернулли.
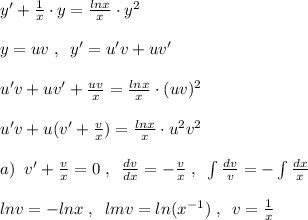
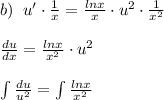
![\int u^{-2}\cdot du=\int x^{-2}\cdot lnx\cdot dx\\\\ \Big [u=lnx,\; dv=x^{-2}dx,\; v=\frac{x^{-1}}{-1}=-\frac{1}{x},du=\frac{dx}{x},\; \int u\, dv=uv-\int v\, du\Big ]\\\\\frac{u^{-1}}{-1}=lnx\cdot (-\frac{1}{x})+\int \frac{dx}{x^2}\\\\-\frac{1}{u}=-\frac{lnx}{x}-\frac{1}{x}-C\; \; \; \Rightarrow \; \; \; \frac{1}{u}=\frac{lnx}{x} +\frac{1}{x}+C\\\\ \frac{1}{u}= \frac{lnx+1+Cx}{x} \; \; \; \Rightarrow \; \; \; u= \frac{x}{lnx+1+Cx}](/tpl/images/0770/0852/46697.png)
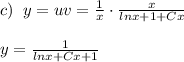
ПОКАЗАТЬ ОТВЕТЫ
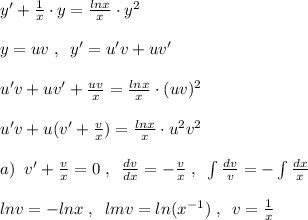
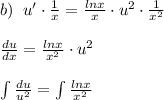
![\int u^{-2}\cdot du=\int x^{-2}\cdot lnx\cdot dx\\\\ \Big [u=lnx,\; dv=x^{-2}dx,\; v=\frac{x^{-1}}{-1}=-\frac{1}{x},du=\frac{dx}{x},\; \int u\, dv=uv-\int v\, du\Big ]\\\\\frac{u^{-1}}{-1}=lnx\cdot (-\frac{1}{x})+\int \frac{dx}{x^2}\\\\-\frac{1}{u}=-\frac{lnx}{x}-\frac{1}{x}-C\; \; \; \Rightarrow \; \; \; \frac{1}{u}=\frac{lnx}{x} +\frac{1}{x}+C\\\\ \frac{1}{u}= \frac{lnx+1+Cx}{x} \; \; \; \Rightarrow \; \; \; u= \frac{x}{lnx+1+Cx}](/tpl/images/0770/0852/46697.png)
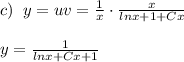
Другие вопросы по теме Алгебра
Популярные вопросы
- Как в стихотворении Ивана Алексеевича Бунина противопоставлены...
2 - Природные зоны размещены в соответсвии:1) с принципом широтной...
2 - Чи можуть екосистеми залишатися незмінними?...
1 - Найти равные треугольники (задания 2-6)...
1 - Укажите, куда впадают реки Евразии, закрасив фигуры соответствующим...
2 - Рассчитай, сколько энергии поступает на 2-й трофический уровень...
3 - решить Закон Кулона. Уже несколько вариантов перебрала и ничего...
2 - Обчислити площу круга діаметром 4 см...
3 - ответить на во по рассказу Платонова Возвращение .Желательно дать...
1 - король,честолюбец,пьяница,фонарщик,географ, Делец . 1.Чем занимается...
3