Впачке 10 тетрадей, причем половина из них в клетку, а остальные в линейку. найти вероятность того, что среди одновременно наудачу вынутых из пачки трех тетрадей окажется не более двух тетрадей в клетку.

Ответы

andreikoval07 02.10.2020 06:16

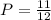ответ: $P=\frac{11}{12}$ .

Объяснение:

Всего 5 тетрадей в клетку и 5 тетрадей в линейку.

Вынимают из пачки, в которой 10 тетрадей, 3 тетради.

Должно оказаться не более 2-х тетрадей в клетку, то есть или 0 тетрадей в клетку и 3 тетради в линейку, или 1 тетрадь в клетку и 2 тетради в линейку, или 2 тетради в клетку и 1 тетрадь в линейку.

$m=C_5^0\cdot C_5^3+C_5^1\cdot C_5^2+C^2_5\cdot C_5^1=1\cdot \frac{5\cdot 4\cdot 3}{3!}+5\cdot \frac{5\cdot 4}{2!}+\frac{5\cdot 4}{2!}\cdot 5=\\\\=10+50+50=110\\\\n=C_{10}^3=\frac{10\cdot 9\cdot 8}{3!}=120\\\\P=\frac{m}{n}=\frac{110}{120}=\frac{11}{12}\approx 0,917$