1. Алгебра
  2. Вот такая система уравнений,

Вот такая система уравнений, сложно 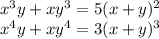x {}^{3} y + xy {}^{3} = 5(x + y) {}^{2} \\ x {}^{4}y + xy {}^{4} = 3(x + y) {}^{3}
, решить ​

trinadsyear trinadsyear    2   10.08.2021 21:43    0

Ответы
Jamik1008 Jamik1008  10.09.2021 00:32

Рассмотрим случай, когда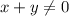 x+y\neq 0

Умножим первое уравнение на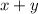  x+y, если в результате решения системы получим решение, в котором 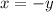x = -y, то исключаем его.

(x^3y + xy^3)(x+y) = 5(x+y)^3\\x^4y + xy^4 + x^3y^2 + y^3x^2 = 5(x+y)^3

Используя второе уравнение системы, получаем:

x^2y^2(x+y) = 2(x+y)^3

Поскольку: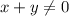 x+y\neq 0

x^2y^2 = 2(x+y)^2\\

Преобразуем первое уравнение системы:

xy(x^2+y^2) = 5(x+y)^2\\xy(x^2+y^2 + 2xy) = 5(x+y)^2 + 2x^2y^2\\xy(x+y)^2 = 9(x+y)^2\\xy = 9

Откуда получаем:

(x+y)^2 = \frac{81}{2} \\(x-y)^2 = (x+y)^2 - 4xy = \frac{81}{2} - 36 = \frac{9}{2}

x+y = +-\frac{9\sqrt{2} }{2} \\x-y =+-\frac{3\sqrt{2} }{2}

x_{1} = (9+3)\frac{\sqrt{2} }{4} = 3\sqrt{2} \\y_{1} = (9 - 3)\frac{\sqrt{2} }{4} = \frac{3\sqrt{2} }{2} \\x_{2} = (-9+3)\frac{\sqrt{2} }{4} = -\frac{3\sqrt{2}}{2} \\y_{2} = (-9 - 3)\frac{\sqrt{2} }{4} = -3\sqrt{2} \\x_{3} = (-9-3)\frac{\sqrt{2} }{4} = -3\sqrt{2} \\y_{3} = (-9 + 3)\frac{\sqrt{2} }{4} = -\frac{3\sqrt{2} }{2}\\x_{4} = (9-3)\frac{\sqrt{2} }{4} = \frac{3\sqrt{2} }{2}\\y_{4} = (9 + 3)\frac{\sqrt{2} }{4} = 3\sqrt{2} \\

Осталось рассмотреть случай: x=-y

Подставляя в первое уравнение системы получаем:

xy(x^2+y^2) = 0\\x= y =0

Нетрудно убедится, что они удовлетворяют и второму уравнению системы:

x_{5} = y_{5} = 0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
frnkiero1133324 frnkiero1133324  01.02.2021 01:40
Найдите длину окружности l пруда, если известно, что площадь пруда равна 7,29π м2. ответ дайте в виде дроби...
ГолубьФедя ГолубьФедя  01.02.2021 01:30
Какой одночлен следует поставить вместо звездочки что бы полученное выражение можно было представить в виде квадрата двучлена. 1)*+30m^3n^2+9n^4. 2)a^4-0,8a^6+*. 3)*-ab+1/25b^2....
фриск2 фриск2  01.02.2021 01:28
4.Решите задачу,выделяется три этапа математического моделирования: сторона прямоугольника как7:6,а его площадь равна168см*Найдите стороны прямоугольника.​...
slavabancov slavabancov  01.02.2021 01:25
Мария Ивановна потратила за день 120 руб. на проезд 320 руб. на продукты в супермаркете пятую часть израсходовано за день суммы на обед в кафетерии и 25% на лекарства Сколько...
rumtum rumtum  01.02.2021 01:15
Відповідь і розв язки завдань до ть будьласочка ​...
olaseve2007ls olaseve2007ls  06.02.2022 02:10
Найти производную функцию F(x) =(4x+7)^3 y=3e^3x+2sinx...
Бетти2004 Бетти2004  06.02.2022 02:15
У 2018 році в країні побудували один сучасний сміттєпереробний комплекс;У кожному наступному році планується побудувати на три таких комплекси більше,ніж у попередньому.Скільки...
Nastya20081505 Nastya20081505  06.02.2022 02:27
Розкласти на множники: a) a³ +8; б) 27 + m³; в) 1 - р³;г) c³ - 64x³;ґ) n⁶ - 1; д) 27a³ + b³....
АняЕнот АняЕнот  13.07.2019 21:30
Косинус тупого угла равен - 1 / корень из 10 . найдите тангенс этого угла...
maktanya563 maktanya563  13.07.2019 21:30
8√2-4√18-√50 11√3-7√48-√75 √48р+√36+√27р √25+3√90а-2√40а √5*(2√5+5√8) √3*(5√3-7√6) (3√7-1)(3√7+1) (1-4√3)в квадрате (2√7+1)в квадрате √3(√6+√3)-7\2√8...

Популярные вопросы