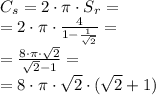.(Вокружность радиуса 4 см вписан квадрат, в который снова вписана окружность, и т. д. найдите сумму длин всех таких окружностей.).

Ответы

Znanija027 23.05.2020 15:14

Если вписать квадрат в окуржность, то его диагональ будет диаметром этой окружности (угол опирающийся на диаметр - прямой). Таким образом длина диагонали квадрата вписанного в окружность: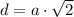 $d = a \cdot \sqrt{2}$ , где a - сторона квадрата. Так как диагональ есть диаметр то она равна двум радиусам: 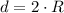$d = 2 \cdot R$ . Тогда выразим длину стороны квадрата: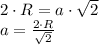 $2 \cdot R = a \cdot \sqrt{2} \\a = \frac{2 \cdot R}{\sqrt{2}}$

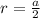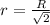Если вписать окружность в квадрат, то ее радиус будет равен половине стороны квадрата: $r = \frac{a}{2}$ . Подставив предыдущую формулу в данную, получим: $r = \frac{R}{\sqrt{2}}$ .

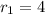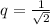Таким образом мы получили бесконечно убывающую геометрическую прогрессию радиусов окружностей. Первый элемент r_1 = 4 , знаменатель прогресии $q = \frac{1}{\sqrt{2}}$ .

Сумма всех радиусов равна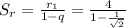 $S_r = \frac{r_1}{1 - q } = \frac{4}{1 - \frac{1}{\sqrt{2}}}$ .

Тогда сумма длин всех окружностей: $C_s = 2 \cdot \pi \cdot S_r = \\= 2 \cdot \pi \cdot \frac{4}{1 - \frac{1}{\sqrt{2}}} = \\ = \frac{8 \cdot \pi \cdot \sqrt{2}}{\sqrt{2} - 1} = \\ = 8 \cdot \pi \cdot \sqrt{2} \cdot (\sqrt{2} + 1)$