Вместо n надо подставить 8
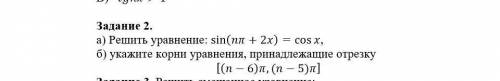
Другие вопросы по теме Алгебра
Популярные вопросы
- Как называется воздушное поверхность...
2 - Восновании прямой треугольной призмы лежит треугольник с сторонами 13,20,21.найти:...
3 - Визначити густину за гелієм та масу 1л газової суміші, що містить за об ємом...
3 - Визначити густину за воднем газової суміші, що містить 80 % водню і 20 %...
1 - Если из задуманного трехзначного числа вычесть это же число,только перевёрнутое...
1 - Расположились, радостные, полянке. выполните морфемный и словообразовательный...
1 - Внешний угол при основании равнобедренного треугольника равен 94 градусам....
2 - 1)34•корень из 3•tg330; 2)21•cos177 градусов/cos3 градусов; 3)30•tg9градусов•tg99градусов;...
1 - Переведите слово қанағаттандырылмағандықтарыңыздан...
2 - Относительная плотность сгоревшего вещества по кислороду равна 0,875. какова...
2
a)
б)
Объяснение:
a)
sin (8π + 2x) = cos x
sin 2x = cos x
2 sin x · cos x - cos x = 0
cos x (2sin x - 1) = 0
1) cos x = 0
2) 2sin x - 1 = 0
sin x = 1/2
б) х∈ [2π; 3π]
1)
k = 2
2)
m = 1
3)
n = 1