Вквадратном уравнении 3x^2+bx+15=0 найдите b, если известно, что корни уравнения – целые числа.

Ответы

Karinavalitova1 11.10.2020 02:59

18,-18

Объяснение:

Используем теорему Виета.

Приведем уравнение к виду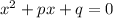 $x^{2} + px + q = 0$

$3x^{2} +bx+15=0\\x^{2} +\frac{b}{3} x+5=0$

По теореме Виета:

x1 + x2 = −p

x1 · x2 = q

Получается:

x1 + x2 = -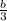 $\frac{b}{3}$

x1 · x2 = 5

Так как корни - целые числа, то x1 · x2 = 5 только при корнях 1 и 5 или -1 и -5.

Значит, либо:

$-\frac{b}{3} =1+5\\b=-18$

либо:

$-\frac{b}{3} = -1 - 5\\b=18$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

alina17anilaalina 29.04.2020 12:39

alinamalina37544 29.04.2020 12:39

jakupbekova860 29.04.2020 12:39

Выразите x через y и y через x1) 3x-5y=18 2) 7y+2x=-213) 9x+3y=11...

lobanovartem2 29.04.2020 12:39

Построить график функции:у=4х²+4х-3...

marsik261 29.04.2020 12:40

14251714 29.04.2020 12:40

Тест по алгебре 1 часть буквой, 2 часть расписать...

fcnhff7 10.09.2020 22:17

тимаинна 10.09.2020 22:14

BlackWolf05 10.09.2020 22:21

lolkek6969 10.09.2020 22:16

3(1,2), 4(a, б), 5( а,б), 7(1,2), 8(1)...