Вирішіть рівняння х^4+x^3-8x+1 = 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Тема урока: «Г.Х. Андерсен. Сказка «Соловей» Домашнее задание:...
1 - 2. Навести конкретні приклади ритмічностігеографічної оболонки....
1 - (0,12-10-0,216:0,216):0,03...
2 - Яку масу аніліну можна добути зі 150г технічного нітробензину,...
1 - Дан треугольник геометрия 8 класс...
2 - 1. Целостность организмов животных и растений обеспечивается...
2 - Що спільного у назві й сюжеті п’єси Дж. Б. Шоу та сюжеті античного...
3 - В равнобедренном треугольнике АВС стороны АВ=ВС, АР и СН - высоты....
2 - Расскажите о распространения плодов и семян...
1 - Характеристика машиніста Лукаса...
1
Решение уравнения 4-ой степени методом Феррари.
Пусть имеется общий уравнения четвертной степени
В данном случае a = 1; b = 0; c = -8; d = 1.
Выполним замену, пусть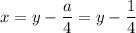 , получим
, получим
p = -3/8; q = -63/8; r = 765/256.
Подставляя коэффициенты в уравнение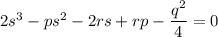
Мы получим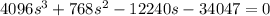 и решим это уравнение методом разложения на множителей
и решим это уравнение методом разложения на множителей
Получаем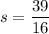
Это уравнение решений не имеет, так как D = -442368 < 0.
Далее подставляем коэффициент в квадратное уравнение вида
Выполнив обратную замену, получим ответ
Объяснение:
Выделим полную четвертую степень:
Сделаем замену: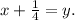
Откуда: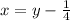
Уравнение примет вид:
Домножим обе части уравнения на 256 и сделаем замену m = 4y;
Очевидно, второй множитель не имеет действительных решений. Значит, t = 42. Напомню, что это такое число, при котором правая часть - полный квадрат. Подставим его.
Рассмотрим первый множитель:
Аналогично рассмотрев второй множитель обнаружим, что D/4 < 0, а значит, действительных корней нет.