В урне 5 белых и 3 черных шаров.
а)Из урны вынимают одновременно два шара. Найдите вероятность того, что они одинакового цвета.
б)Какое событие, при условии, что из урны вынимают одновременно два шара, более вероятно: A - "шары одного цвета", В - "шары разных цветов"?
Другие вопросы по теме Алгебра
Популярные вопросы
- Скільки ланок C6H10O5 міститься в целюлозі якщо її молярна маса 6000000?...
1 - Запишіть формотворчі, словотворчі та модальні частки у три колонки. Лише, аби-,...
2 - ( ) Сказ «Каменный цветок» (Почему жизнь Данилы можно назвать тяжелой? Почему...
1 - Тестування за творчістю Лесі Українки...
3 - Точка А (-19; 23) розташована у 1) IV чверті2) III чверті3) II чверті4) I чверті...
1 - описать Индийский океан по плану....
2 - 1 місяця білка з їла27% запасу горіхів,2-го 23%,3-го 29%.Після цього в неї залишилось...
1 - height. 1 Complete the sentences. 1 David isn t tall or short. He s 2 Grandad...
1 - Дарство В) Древняя Индия А)ассирийское государство Б) Древний Египет Г) Древняя...
3 - Небольшой рассказ о природе на казахском языке шесть предложений ....
1
а)
Благоприятное число событий складывается из двух: число выбрать 2 шарика из 5 белых и число выбрать 2 шарика из 3 черных. Общее количество событий: выбрать 2 шарика из 8.
б)
Вероятность события А уже вычислена в предыдущем пункте. Заметим, что если шары не одного цвета, то они разных цветов. Значит, события А и В противоположны. Пользуясь этим, найдем вероятность события В:
Так как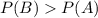 , то вероятнее достать шары разных цветов, чем шары одного цвета.
, то вероятнее достать шары разных цветов, чем шары одного цвета.