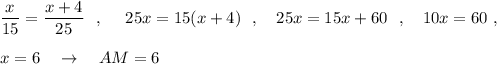В прямоугольном треугольнике ABC с прямым углом C проведена Прямая KM параллельная стороне CB треугольника, Точки K и M лежат на сторонах CA и BA треугольника АВС соответственно. Найдите длину отрезка АМ, если известно, что СВ=25, КМ=15, а длина отрезка АВ на 4 больше длины отрезка АМ.
Другие вопросы по теме Алгебра
Популярные вопросы
- Учеловека карий цвет глаз(а) и владеть правой рукой(в) наследуется...
3 - Сколько значений имеет выражение 20 -а?...
3 - Описания особенностей жизни в тайге...
1 - Who are the druids? why is halloween a special day? which season...
3 - Из двух пунктов а и в расстояние между которыми равно 21 км одновременно...
3 - Небе какой это падеж дательный если нет напишите правильный ответ...
1 - Магнитный поток,пронизывающий замкнутый контур проводника сопротивлением...
2 - Сочинение-миниатюра сердце кая или забытый лист объём 10-12 предложений...
3 - 27 9 3=729 27 9 3=1 27 9 3=54 27 9 3=240 27 9 3=9 27 9 3=10 запиши...
1 - Нужно сочинение на тему за что можно любить свою родину...
3
ΔAKM подобен ΔАВС ⇒