Уравнение на скрине объяснений, а не ответ.
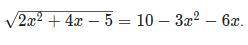
Другие вопросы по теме Алгебра
Популярные вопросы
- Мне нужно написать сочинение на тему после кратко и ясно...
2 - Яке значення головного мозку для організму людини...
1 - Из пяти букв разрезной азбуки составлено слово крыша . ребенок рассыпал буквы...
1 - Известны границы длины m и ширины n комнаты прямоугольной формы (в метрах):...
2 - Составить реакции: c2h5oh+n2= c2h5oh+k2co3=...
2 - ! расставьте в последовательности а) сражение под прохоровкой б) смоленское...
1 - Сообщение о маяковском(желательно не большое просто в тетрадку переписывать...
2 - Вдвух ящиках всего 112кг яблок, причём в одном из них в 3 раза больше, чем...
2 - Впрямоугольном треугольнике abc проведена медиана cm. найти ab если cm=1....
2 - Придумал и запиши рассказ об отношений мальчика и собачки. 5-6 предложений...
3
-3; 1
Объяснение:
Замена:
Рассмотрим правую часть уравнения:
Тогда:
Приведу другое решение задачи:
Учитывая, что![x\in\left[\dfrac{-3-\sqrt{39}}{3};\; \dfrac{-3+\sqrt{39}}{3}\right]](/tpl/images/1330/0875/8f3dd.png) , а если в приблизительных значениях, то
, а если в приблизительных значениях, то ![x\in\left[\approx-3,08;\; \approx1,08\right]](/tpl/images/1330/0875/4e11f.png) :
:
x1=1
x2=-3
Объяснение:
ОДЗ писать нет смысла , ибо оно иррациональное.
Сделаем замену :
√(2*x^2 +4x-5) =t>=0
Тогда :
10-3*x^2-6*x = -3*(t^2+5)/2 +10
Уравнение принимает вид :
t = -3*(t^2+5)/2 +10
2t= -3*t^2 -15 +20
3*t^2+2t-5=0
По теореме Виета :
t1=1
t2=-5/3 < 0 ( не подходит)
√(2*x^2+4x-5) = 1
2*x^2+4x-5=1
2*x^2+4*x-6=0
x^2+2x-3=0
По теореме Виета :
x1=1
x2=-3
Поскольку ОДЗ мы не искали ,сделаем проверку :
1) x1=1
√(2+4-5) = 10-3-6
1=1 (верно)
2) x2=-3
√(18-12-5) = 10 -27 +18
1=1 (верно)