Укажите соответствующий вывод для каждого неравенства. Обоснуйте свой ответ.
а) 2х2 -х +1 ≥ 0
b) х2 -6х + 9 > 0
c) -х2 -3х +4 ≤ 0
d) –х2 +9 < 0
1) Неравенство не имеет решений.
2) Решением неравенства является вся числовая прямая.
3) Решением неравенства является одна точка.
4) Решением неравенства является закрытый промежуток.
5) Решением неравенства является открытый промежуток.
6) Решением неравенства является объединение двух промежутков.
(решите
Другие вопросы по теме Алгебра
Популярные вопросы
- Птицы подхватыали на лету отдельные струи дождя и неслись с ними вперёд,...
3 - 5предложений, в каждом предложении 2 времени: past simple и present perfect....
1 - Заполните таблицу, если величина у обратно пропорциональна величине х. x:...
3 - Впалатку 8 коробок яблок по 9 кг в каждой и столько же коробок груш по 7...
1 - Вне неразвернутого угла авс проведены параллельные лучи ad и ce найдите...
1 - Укажите обособленные и необособленные определения. 1) молодой месяц, светивший...
3 - ответьте на вопрос по обществознанию почему в россии звание „гражданин”...
3 - Составте 10 предложений на татарском про кота или семью, с переводом...
3 - Написать программу вычисления площади и периметра трапеции. 90 ....
1 - Які речення можна скласти зі словом їда...
2
ответ: №1 неравенство не имеет ДЕЙСТВИТЕЛЬНЫХ решений.
ответ: №6 .
P.S. Если бы в пункте b) знак был бы нестрогий, то ответом был бы №2 :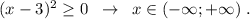
ответ: №6 .
ответ: №6 .