Укажите позволяющий установить взаимно однозначное соответствие: а) между множеством четных натуральных чисел и множеством нечетных натуральных чисел; б) множеством квадратов натуральных чисел и множеством кубов натуральных чисел.
Другие вопросы по теме Алгебра
Популярные вопросы
- 3 тур 19 и 20 задание помгитее...
3 - Из пружинного пистолета делают выстрел в горизонтальном направлении....
1 - Who do we usually send formal emails to? Choose the correct answers...
3 - Психологические аспекты защиты прав и интересов детей в возрасте...
3 - 3(х+65)+33=200 очень нужно...
2 - написать 5 предложений на тему don t и 5 на doesn t...
3 - В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7,...
3 - Напишите название этих систем...
2 - 4-тапсырма. Мәтін мазмұны бойынша өз ойыңмен бөліс. - Менің білгеніме...
1 - Эпитеты и метафоры в стихотворения птичка Пушкин В чужбине свято...
2
а)
Множество четных натуральных чисел: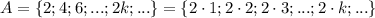
Множество нечетных натуральных чисел: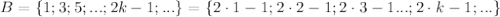
Можно заметить, что если от любого элемента множества А отнять 1, то получится элемент множества B.
Тогда, если x - четное натуральное число, y - нечетное натуральное число, то:
б)
Множество квадратов натуральных чисел: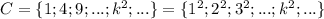
Множество кубов натуральных чисел: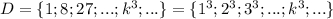
Можно заметить, что если из любого элемента множества C извлечь квадратный корень и получившееся число возвести в куб, то получится элемент множества D.
Тогда, если x - квадрат натурального числа, y - куб натурального числа, то: