Тригонометрия 2sin^2x+√2sinx-10sinx-5√2=0
Ответы
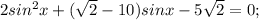
![sinx=t;t \in[-1;1];](/tpl/images/0371/5247/a7746.png)
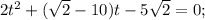
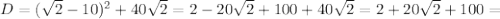
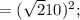
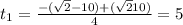 - посторонний корень
- посторонний корень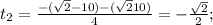
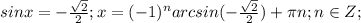
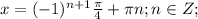
Другие вопросы по теме Алгебра
Популярные вопросы
- Что называют белым золотом и черным золотом ? где раки зимуют?...
1 - Что такое землянуха? порожник? делаю ломаносавский...
2 - Подготовиться к №1 на весаз, на левой чаше з пакета с мукой, а на правой...
1 - Найдите сумму всех целых чисел от -14 до 20,включая 20...
1 - Закон менделеева-клапейрона можно записать в виде pv = νrt, где p —...
3 - Іть дуже потрібно де утворюються сперматозоони?...
2 - Почвенная карта территории казахстана...
3 - Нужно сочинение рассуждение всегда ли нужно следовать моде 50 за сочинение...
3 - Вшкольном саду 60 деревьев: 1/3деревьев-яблони,1/4-груш.сколько в саду...
3 - Вкаждой группе даны 2 определения одного и того-же слова.догадайся,кто...
1