Три числа являются последовательными членами арифметической прогрессии.сумма их равна 33, а произведение 1287.найти эти числа

1) 9;11;13. 2) 13;11;9.

Объяснение:

Пусть  последовательные члены арифметической прогрессии это x,y и z.

Тогда воспользуемся условием и характеристическим свойством арифметической прогрессии 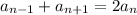  ( )  и составим систему уравнений:

Решим квадратное уравнение :

Если x=9, то z=22-9=13;

Если x=13 , то z=22-13=9 .

Тогда получим  первые три числа 9; 11 и 13 и вторые 13;11 и 9.

Три числа являются последовательными членами арифметической прогрессии. Сумма их равна 33, а произведение 1287. Найти эти числа.

Запишем условие удобным для решения образом:

первое число из 3-х в арифметической прогрессии

- второе число

- третье число

Значит, их сумма равна:

Зная, что ⇒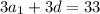

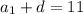
А произведение:

Зная, что оно равно 1287 можем составить систему уравнений. Для удобства вычислений заменим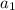 на x. Имеем:

(11-d)(11-d+d)(11-d+2d)=1287

(11-d)*11(11+d)=1287

(121-d²)*11=1287

1331-11d²=1287

-11d²=-44

d²=4

d=+-2

Уже ясно, что вариантов ответа будет 2:

Первый вариант:

1) В том случае, если d = 2, имеем:

Имеем: 9; 11; 13

Второй вариант:

2) В том случае, если d = -2, имеем:

Имеем: 13; 11; 9

ответ: 9; 11; 13 и 13; 11; 9