Тоже нужно докажите что выражение 8 в пятой степени + 2 в тринадцатой степени делиться на 10.

Question

Алгебра: Тоже нужно докажите что выражение 8 в пятой степени + 2 в тринадцатой степени делиться на 10.

sotela546hgjUlia · Answer

Число 8 в первой степени оканчивается на 8, во второй - на 4, в третьей - на 2, в четвёртой - на 6, в пятой - опять на 8.

Число 2 в первой степени оканчивается на 2, во второй - на 4, в третьей - на 8, в четвёртой - на 6, в пятой - опять на 2, в шестой - снова на 4 и т.д. То есть соблюдается определённая цикличность. А значит, 2 в тринадцатой степени будет оканчиваться на 2.

2+8=10, следовательно, сумма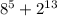 $8^5+2^{13}$ будет оканчиваться на 0, а значит, делиться на 10 без остатка, что и требовалось доказать.

Тоже нужно докажите что выражение 8 в пятой степени + 2 в тринадцатой степени делиться на 10.

Популярные вопросы