​

Объяснение: Ищем ОДЗ. Одновременно должны выполняться три условия :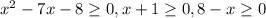

Решением первого неравенства является объединение полуинтервалов (-∞; -1] ∪ [8; +∞) (вложение), решение второго - [-1; +∞), решение третьего - (-∞; 8]. Условия выполняются одновременно, поэтому нужно искать пересечение этих промежутков - им является множество {-1; 8}.

Так как ОДЗ удовлетворяют только два числа, можем спокойно их подставить в наше неравенство и посмотреть, какие из них являются решением.

При х = -1 получаем: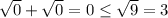 - верное неравенство. х = -1 - решение.

При х = 8 получаем: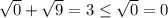 - неверное неравенство. Следовательно, х = 8 не является решением.

Все случаи перебрали. Запишем ответ.

ОТВЕТ: -1.