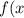=\sqrt{6+2x} -\frac{3x}{x-5})
найти область определения функции
Другие вопросы по теме Алгебра
Популярные вопросы
- At the special colebration ...
2 - На сторінці книги друкований текст повинен займати 432 см. Поля зверху...
2 - 2. Вершины треугольника KMN имеют координаты К(8; 3; 5), М(14; 1;0),...
2 - по литературе на тему Зимнее утро А С Пушкина. выразительно прочитайте...
3 - Сочинение по теме в мире глухих и звонких согласных...
1 - 1.Как переносятся питательные вещества у растений? 2.Что переносить...
1 - Что образуется в результате реакции нейтрализации? а) Соль и вода;...
1 - Розв язати системи нерівностей {2t-1≥0 4-2t≤0...
3 - Задание №4. Расставь знаки препинания и запиши предложения в соответствии...
3 - А)чему равен диаметр круга если его радиус 6см 5мм Б) Чему равен радиус...
3
Объяснение:
1) Поменять порядок слагаемых или множителей:
2) Разделите функцию на части:
2) Найдите все значения, для которых подкоренное выражение положительно или 0. Область определения - все действительные числа. Найдите все значения, для которых знаменатель отличен от 0:
х принадлежит R
х принадлежит R \ {5}
х принадлежит R
х принадлежит R
3) Найти пересечение:
х принадлежит [-3;5) (знак на фото) (5; до +бесконечность)