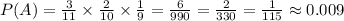Теория вероятностей элементы комбинаторики
Другие вопросы по теме Алгебра
Популярные вопросы
- Два из легких стержней длиной L1 и L2 соединены шарнирно в точке...
1 - 1.19. Вычислите: 1) -5² +(-2)⁴; 2)3⁴ - ( 2/5)² ×6 1/4; 3) 0,2 ×...
3 - Сообщение о любимой книге Дубровский а с Пушкин ...
3 - Сравните Бумына кагана и Бумына тардуш МНЕ....
1 - 1/8 Мбайтте сколько Кбайтта?...
1 - До ть будь ласка (( через точку К, проведено до кола дотичну KA...
2 - Что можно узнать благодаря интонации? 1) Настроение человека 2)...
2 - Обчислити масову частку елементів у формулі Zn(NO3)2...
1 - 1) Not many people believe that Mallory msde/reached it to the top...
1 - Укр мова анал.слова яблучко...
1
0.009 с точностью до тысячных
Объяснение:
Поступим следующим образом. Вероятность того, что наудачу выбранный человек из 11 окажется мужчиной, равна 3/11.
Теперь повторим испытание, убрав выбранного мужчину из выборки. Тогда вероятность выбрать наудачу мужчину из 10 человек окажется равной 2/10.
Соответственно 1/9 - вероятность того, что третий подряд мужчина окажется в выборе.
По правилу умножения вероятностей, получаем