Теңсіздіктің дәрежесін және айнымалылар санын анықтаңдар: 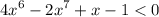
һ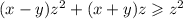
за
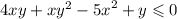
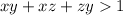
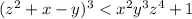
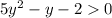
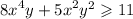
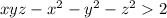
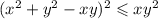
Ответы
Показать ответы (3)
Другие вопросы по теме Алгебра
Популярные вопросы
- Построить график функции -x^2+3x-2=0...
2 - Холодно становиться холодно! холод не так страшен тем животным,у которых...
3 - Сократить дроб 63m во 2 степени х в 3 степени 42m в 5 степени х...
3 - Площадь прямоугольника равна 24 см2. одна его сторона в 1,5 раза больше...
2 - Яма,оля,пень.я.фея.он,ты.выпиши слова,в которых одинаковое количество...
3 - Составьте программу,которая определяет,является ли введеное число...
2 - Вмерную колбу объёмом 500 мл поместили 10 г медного купороса cuso4*5h2o...
1 - Всахарном сиропе отношение массы воды к массе сахара 17/3 масса воды...
2 - Нужно сделать в паскаль авс самолет летит из пункта а в пункт б со...
2 - Составить уравнение, корнем которого является число а)3; б)-4...
2