1. Алгебра
  2. Сумма 8 и 6 члена арифметической

Сумма 8 и 6 члена арифметической прогрессии=16 а произведение 2 и 12=-36. найти разность и первый член прогрессий.

shariktop000 shariktop000    2   02.06.2019 05:00    1

Ответы
donaldavis1337 donaldavis1337  01.10.2020 17:10

Из условия: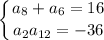 \displaystyle \left \{ {{a_8+a_6=16} \atop {a_2a_{12}=-36}} \right.

Используем формулу n-го члена арифметической прогрессии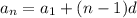 a_n=a_1+(n-1)d, имеем

\displaystyle \left \{ {{a_1+7d+a_1+5d=16} \atop {(a_1+d)(a_1+11d)=-36}} \right.~~~\Rightarrow~~~\left \{ {{a_1+6d=8} \atop {(a_1+6d-5d)(a_1+6d+5d)=-36}} \right.\\ \\ (8-5d)(8+5d)=-36\\ \\ 64-25d^2=-36\\ \\ 25d^2=100\\ \\ d^2=4\\ \\ d=\pm2


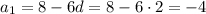
Если d=2, то a_1=8-6d=8-6\cdot2=-4

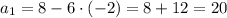
Если d=-2, то a_1=8-6\cdot(-2)=8+12=20



ответ: a₁=-4 и d=2 или a₁=20 и d=-2.

ПОКАЗАТЬ ОТВЕТЫ
bua20 bua20  01.10.2020 17:10

Выразим a₆, a₈, a₂ и a₁₂ через формулу n-ого члена арифметической прогрессии.

aₙ = a₁ + (n-1)×d, где d - разность арифметической прогрессии, n - номер

a_6 = a_1 + 5d\\\\a_8 = a_1 + 7d\\\\a_2 = a_1 + d \\\\a_{12} = a_1 + 11d

Составим систему из двух уравнений

\left \{\begin{array}{lcl} {{a_6+a_8=16} \\ {a_2\cdot a_{12}=-36}}\end{array} \right. \\\\\\\left \{\begin{array}{lcl} {{a_1+5d+a_1+7d=16} \\ {(a_1+d)\cdot (a_1 + 11d)=-36}}\end{array}\right.\\\\\\\left \{\begin{array}{lcl}{{2a_1+12d=16\;\;|:2} \\ {((a_1+6d)-5d)\cdot ((a_1 + 6d)+5d)=-36}}\end{array} \right.\\\\\\\left \{\begin{array}{lcl} {{a_1+6d=8} \\ {(a_1+6d)^2-25d^2=-36}}\end{array} \right.


\left \{\begin{array}{lcl} {{a_1+6d=8} \\ {\underbrace{(a_1+6d)^2}_{8^2}-25d^2=-36}}\end{array} \right.\\\\\\\left \{\begin{array}{lcl} {{a_1+6d=8} \\ {25d^2=100}}\end{array} \right.\\\\\\\left \{\begin{array}{lcl} {{a_1+6d=8} \\ {d=\pm 2}}\end{array} \right.

Если d = 2, то a₁ = 8 - 6d = 8 - 12 = -4

Если d = -2, то a₁ = 8 + 12 = 20

ответ: Если d = -2, то a₁ = 20, а если d = 2, то a₁ = -4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
benblast benblast  27.12.2020 13:00
Я не понимаю как получили ответ? И 6^10 это сколько...
lolgg2 lolgg2  27.12.2020 13:01
Окно состоит из трех прямоугольных частей, размеры которых указаны на рисунке. Выразить площадь всего окна S и площадь каждой частиS1,S2,S3 через a и b​...
VadimqaFL VadimqaFL  27.12.2020 13:08
Добрый день Нужно с решением,...
пага45 пага45  09.07.2019 02:50
Довести ,що різниця двоцифрового числа і числа записаного тими самими цифрами,але в зворотному порядку,ділиться на 9...
clykovsa clykovsa  09.07.2019 02:50
(-1/3m в )(4nm) решите нужно сегодня владимир б реши надо...
cfgcgj cfgcgj  09.07.2019 02:50
Y=x^2+3/x^2+1 1) найти область определения 2) найти точки пересечения графика с осями координат( если это возможно) 3) определить чётность и нечётность функции 4)...
Doktor77 Doktor77  09.07.2019 02:50
Сколько существует трехзначных чисел в записи которых каждая цифра 1 и 2 встречаются ровно по одному разу...
sanakajpak sanakajpak  15.02.2022 01:56
ОЧЕНЬ ВОПРОС:Найдите степень многочлены. а)3b^3c+5b^2c^5-7b+3 б)3b^3c+5b^2c^5-7b+3^8 в)7x^5-x^3+20x-1 г)5^5...
grigoryanoksan grigoryanoksan  15.02.2022 01:59
100 ballov Дано . (4x⁴-2x²+1) ²+ (2x³-x²+2)⁴ Найдите а) степе нь многочлена; б) старший коэффициент и свободный член; в) сумму коэффициентов многочлена; г) сумму...
lyubsretste lyubsretste  15.02.2022 02:00
1)sin(-70градусов)*tg120градусов 2)найти область определения, период и (мәндер жиыны)набор значении вроде) у=sin2x+5...

Популярные вопросы