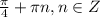Sin(x) + 2 sin^2(x) = sin(2x) + cos (x)
решить
Другие вопросы по теме Алгебра
Популярные вопросы
- (1/8+2/9-1/4)*5 1/7: (7/9-2/3+1/6 по действиям...
2 - Доклад про колядки , стол одияние гадания и тд...
1 - Назар з дитинства хворів, мав серйозні вади серця, через те був...
1 - Как называется этот закон: а+(b+c)=(a+b)+c...
2 - Докажите что выражение 45 x 38 + 45 x 11 делится на 49...
1 - Какие реки,озёра,горы,города есть в вашей местности? сравните...
2 - На красную контарную карту нанести типы почв в казахстане стр...
3 - Зделай на тему простое осложнённое предложение (решённое)...
3 - Как проверить букву ё после шипящих в слове чётко?...
3 - Площадь грани куба, ребро которого равно 10 см.?...
2
Переходим к одному аргументу:
Тогда уравнение можно записать в виде:
Переносим все слагаемые влево и раскладываем на множители группировки:
О т в е т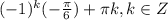 ;
;